Corona theorem
Encyclopedia
In mathematics
, the corona theorem is a result about the spectrum of the bounded holomorphic function
s on the open unit disc, conjectured by and proved by .
The commutative Banach algebra and Hardy space
H∞ consists of the bounded holomorphic function
s on the open unit disc D. Its spectrum S (the closed maximal ideals) contains D as an open subspace because for each z in D there is a maximal ideal
consisting of functions f with
The subspace D cannot make up the entire spectrum S, essentially because the spectrum is a compact space
and D is not. The complement of the closure of D in S was called the corona by , and the corona theorem states that the corona is empty, or in other words the open unit disc D is dense in the spectrum. A more elementary formulation is that elements f1,...,fn generate the unit ideal of H∞ if and only if there is some δ>0 such that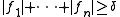
everywhere in the unit ball.
Newman showed that the corona theorem can be reduced to an interpolation problem, which was then proved by Carleson.
In 1979 Thomas Wolff
gave a simplified (but unpublished) proof of the corona theorem, described in and .
Cole later showed that this result cannot be extended to all open Riemann surfaces .
As a by-product, of Carleson's work, the Carleson measure
was invented which itself is a very useful tool in modern function theory. It remains an open question whether there are versions of the corona theorem for every planar domain or for higher-dimensional domains.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the corona theorem is a result about the spectrum of the bounded holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s on the open unit disc, conjectured by and proved by .
The commutative Banach algebra and Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
H∞ consists of the bounded holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s on the open unit disc D. Its spectrum S (the closed maximal ideals) contains D as an open subspace because for each z in D there is a maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
consisting of functions f with
- f(z) = 0.
The subspace D cannot make up the entire spectrum S, essentially because the spectrum is a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and D is not. The complement of the closure of D in S was called the corona by , and the corona theorem states that the corona is empty, or in other words the open unit disc D is dense in the spectrum. A more elementary formulation is that elements f1,...,fn generate the unit ideal of H∞ if and only if there is some δ>0 such that
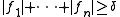everywhere in the unit ball.Newman showed that the corona theorem can be reduced to an interpolation problem, which was then proved by Carleson.
In 1979 Thomas Wolff
Thomas Wolff
Thomas Wolff was a noted mathematician, working primarily in the fields of harmonic analysis, complex analysis, and partial differential equations. As an undergraduate at Harvard University he regularly played poker with his classmate Bill Gates...
gave a simplified (but unpublished) proof of the corona theorem, described in and .
Cole later showed that this result cannot be extended to all open Riemann surfaces .
As a by-product, of Carleson's work, the Carleson measure
Carleson measure
In mathematics, a Carleson measure is a type of measure on subsets of n-dimensional Euclidean space Rn. Roughly speaking, a Carleson measure on a domain Ω is a measure that does not vanish at the boundary of Ω when compared to the surface measure on the boundary of Ω.Carleson measures have many...
was invented which itself is a very useful tool in modern function theory. It remains an open question whether there are versions of the corona theorem for every planar domain or for higher-dimensional domains.