
Correlation immunity
Encyclopedia
In mathematics, the correlation immunity of a Boolean function is a measure of the degree to which its outputs are uncorrelated with some subset of its inputs. Specifically, a Boolean function is said to be correlation-immune of order m if every subset of m or fewer variables in  is statistically independent of the value of
is statistically independent of the value of  .
.
 is
is  -th order correlation immune if for any independent
-th order correlation immune if for any independent  binary random variables
binary random variables 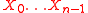 , the random variable
, the random variable  is independent from any random vector
is independent from any random vector  with
with  .
.
as a combining function for linear feedback shift register
s, a Boolean function with low-order correlation-immunity is more susceptible to a correlation attack
than a function with correlation immunity of high order.
Siegenthaler showed that the correlation immunity m of a Boolean function of algebraic degree d of n variables satisfies m + d ≤ n; for a given set of input variables, this means that a high algebraic degree will restrict the maximum possible correlation immunity. Furthermore, if the function is balanced then m + d ≤ n − 1.
 is statistically independent of the value of
is statistically independent of the value of  .
.Definition
A function is
is  -th order correlation immune if for any independent
-th order correlation immune if for any independent  binary random variables
binary random variables 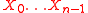 , the random variable
, the random variable  is independent from any random vector
is independent from any random vector  with
with  .
.Results in cryptography
When used in a stream cipherStream cipher
In cryptography, a stream cipher is a symmetric key cipher where plaintext digits are combined with a pseudorandom cipher digit stream . In a stream cipher the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption...
as a combining function for linear feedback shift register
Linear feedback shift register
A linear feedback shift register is a shift register whose input bit is a linear function of its previous state.The most commonly used linear function of single bits is XOR...
s, a Boolean function with low-order correlation-immunity is more susceptible to a correlation attack
Correlation attack
In cryptography, correlation attacks are a class of known plaintext attacks for breaking stream ciphers whose keystream is generated by combining the output of several linear feedback shift registers using a Boolean function...
than a function with correlation immunity of high order.
Siegenthaler showed that the correlation immunity m of a Boolean function of algebraic degree d of n variables satisfies m + d ≤ n; for a given set of input variables, this means that a high algebraic degree will restrict the maximum possible correlation immunity. Furthermore, if the function is balanced then m + d ≤ n − 1.

