Cotlar–Stein lemma
Encyclopedia
In mathematics
, in the field of functional analysis
, the Cotlar–Stein almost orthogonality lemma is named after mathematicians Mischa Cotlar
and Elias Stein. It may be used to obtain information on the operator norm
on an operator, acting from one Hilbert space
into another
when the operator can be decomposed into almost orthogonal pieces.
The original version of this lemma
(for self-adjoint
and mutually commuting operators)
was proved by Mischa Cotlar in 1955 and allowed him to conclude that the Hilbert transform
is a continuous linear operator
in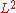
without using the Fourier transform
.
A more general version was proved by Elias Stein.
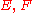be two Hilbert spaces.
Consider a family of operators
, 
,
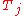with each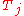
a continuous linear operator
from
to 
.
Denote
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the Cotlar–Stein almost orthogonality lemma is named after mathematicians Mischa Cotlar
and Elias Stein. It may be used to obtain information on the operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
on an operator, acting from one Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
into another
when the operator can be decomposed into almost orthogonal pieces.
The original version of this lemma
(for self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
and mutually commuting operators)
was proved by Mischa Cotlar in 1955 and allowed him to conclude that the Hilbert transform
Hilbert transform
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
is a continuous linear operator
Continuous linear operator
In functional analysis and related areas of mathematics, a continuous linear operator or continuous linear mapping is a continuous linear transformation between topological vector spaces....
in
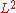
without using the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
.
A more general version was proved by Elias Stein.
Cotlar–Stein almost orthogonality lemma
Let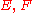 be two Hilbert spaces.Consider a family of operators
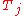, ,with each
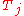
a continuous linear operator
Continuous linear operator
In functional analysis and related areas of mathematics, a continuous linear operator or continuous linear mapping is a continuous linear transformation between topological vector spaces....
from
to .Denote
-
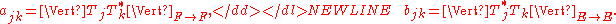
The family of operators
, 
is almost orthogonal if
The Cotlar–Stein lemma states that if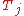
are almost orthogonal,
then the series
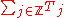
converges in the strong operator topologyStrong operator topologyIn functional analysis, a branch of mathematics, the strong operator topology, often abbreviated SOT, is the weakest locally convex topology on the set of bounded operators on a Hilbert space such that the evaluation map sending an operator T to the real number \|Tx\| is continuous for each vector...
,
and that
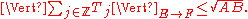
Example
Here is an example of an orthogonal family of operators. Consider the inifite-dimensional matrices
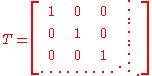
and also
Then
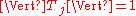for each 
,
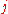hence the series
does not converge in the uniform operator topology.
Yet, since
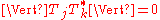
and
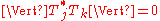
for
,
the Cotlar–Stein almost orthogonality lemma tells us that
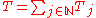
converges in the strong operator topologyStrong operator topologyIn functional analysis, a branch of mathematics, the strong operator topology, often abbreviated SOT, is the weakest locally convex topology on the set of bounded operators on a Hilbert space such that the evaluation map sending an operator T to the real number \|Tx\| is continuous for each vector...
and is bounded by 1.