Coupon collector's problem
Encyclopedia
In probability theory
, the coupon collector's problem describes the "collect all coupons and win" contests. It asks the following question: Suppose that there are n coupon
s, from which coupons are being collected with replacement. What is the probability that more than t sample trials are needed to collect all n coupons? An alternative statement is: Given n coupons, how many coupons do you expect you need to draw with replacement before having drawn each coupon at least once. The mathematical analysis of the problem reveals that the expected number
of trials needed grows as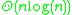
. For example, when n = 50 it takes about 225 trials to collect all 50 coupons.
s. Observe that the probability of collecting a new coupon given i − 1 coupons is pi = (n − i + 1)/n. Therefore, ti has geometric distribution with expectation 1/pi. By the linearity of expectations we have:
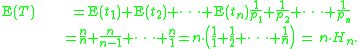
Here Hn is the harmonic number. Using the asymptotics of the harmonic numbers, we obtain:
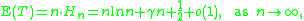
where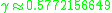
is the Euler–Mascheroni constant
.
Now one can use the Markov inequality to bound the desired probability:
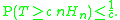
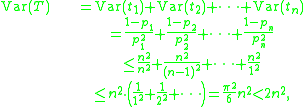
where the last equality uses a value of the Riemann zeta function (see Basel problem
).
Now one can use the Chebyshev inequality to bound the desired probability:
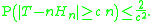
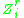denote the event that the 
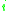-th coupon was not picked in the first 
trials. Then
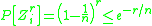
Thus, for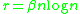
, we have 
.
.
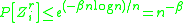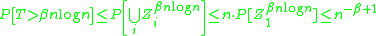
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the coupon collector's problem describes the "collect all coupons and win" contests. It asks the following question: Suppose that there are n coupon
Coupon
In marketing, a coupon is a ticket or document that can be exchanged for a financial discount or rebate when purchasing a product. Customarily, coupons are issued by manufacturers of consumer packaged goods or by retailers, to be used in retail stores as a part of sales promotions...
s, from which coupons are being collected with replacement. What is the probability that more than t sample trials are needed to collect all n coupons? An alternative statement is: Given n coupons, how many coupons do you expect you need to draw with replacement before having drawn each coupon at least once. The mathematical analysis of the problem reveals that the expected number
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of trials needed grows as
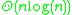. For example, when n = 50 it takes about 225 trials to collect all 50 coupons.Understanding the problem
The key to solving the problem is understanding that it takes very little time to collect the first few coupons. On the other hand, it takes a long time to collect the last few coupons. In fact, for 50 coupons, it takes on average 50 trials to collect the very last coupon after the other 49 coupons have been collected. This is why the expected time to collect all coupons is much longer than 50. The idea now is to split the total time into 50 intervals where the expected time can be calculated.Calculating the expectation
Let T be the time to collect all n coupons, and let ti be the time to collect the i-th coupon after i − 1 coupons have been collected. Think of T and ti as random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s. Observe that the probability of collecting a new coupon given i − 1 coupons is pi = (n − i + 1)/n. Therefore, ti has geometric distribution with expectation 1/pi. By the linearity of expectations we have:
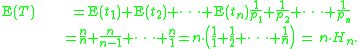
Here Hn is the harmonic number. Using the asymptotics of the harmonic numbers, we obtain:
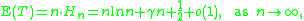
where
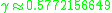is the Euler–Mascheroni constantEuler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
.
Now one can use the Markov inequality to bound the desired probability:
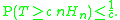
Calculating the variance
Using the independence of random variables ti, we obtain: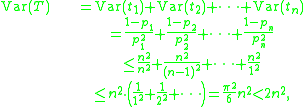where the last equality uses a value of the Riemann zeta function (see Basel problem
Basel problem
The Basel problem is a famous problem in mathematical analysis with relevance to number theory, first posed by Pietro Mengoli in 1644 and solved by Leonhard Euler in 1735. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate...
).
Now one can use the Chebyshev inequality to bound the desired probability:
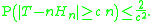
Tail estimates
A different upper bound can be derived from the following observation. Let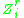 denote the event that the 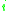-th coupon was not picked in the first trials. Then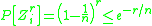Thus, for
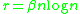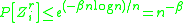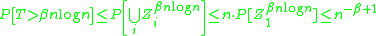
, we have .Connection to probability generating functions
Another combinatorial technique can also be used to resolve the problem: Coupon collector's problem (generating function approach)Coupon collector's problem (generating function approach)
The coupon collector's problem can be solved in several different ways. The generating function approach is a combinatorial technique that allows to obtain precise results....
.
Extensions and generalizations
- ErdősPaul ErdosPaul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and RényiAlfréd RényiAlfréd Rényi was a Hungarian mathematician who made contributions in combinatorics, graph theory, number theory but mostly in probability theory.-Life:...
proved the limit theorem for the distribution of T. This result is a further extension of previous bounds.
-
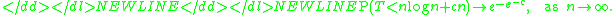
- NewmanDonald J. NewmanDonald J. Newman was an American mathematician and professor, excelling at the Putnam mathematics competition while an undergraduate at City College of New York and New York University, and later receiving his PhD from Harvard University in 1953.- Life and works :Newman was born in Brooklyn, New...
and SheppLawrence SheppLawrence Shepp is an American mathematician, specialising in statistics and computational tomography.Shepp obtained his PhD from Princeton University with a dissertation entitled Recurrent Sums of Random Variables. His advisor was William Feller. He joined Bell Laboratories in 1962. He joined...
found a generalization of the coupon collector's problem when k copies of each coupon needs to be collected. Let Tk be the first time k copies of each coupons are collected. They showed that the expectation in this case satisfies:
-
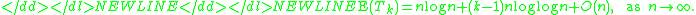
- Here k is fixed. When k = 1 we get the above formula for the expectation.
- Common generalization, also due to Erdős and Rényi:
-
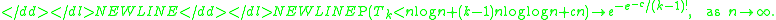
External links
- "Coupon Collector Problem" by Ed Pegg, Jr.Ed Pegg, Jr.Ed Pegg, Jr. is an expert on mathematical puzzles and is a self-described recreational mathematician. He creates puzzles for the Mathematical Association of America online at Ed Pegg, Jr.'s Math Games. His puzzles have also been used by Will Shortz on the puzzle segment of NPR's Weekend Edition...
, the Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. Mathematica package. - Coupon Collector Problem, a simple Java appletJava appletA Java applet is an applet delivered to users in the form of Java bytecode. Java applets can run in a Web browser using a Java Virtual Machine , or in Sun's AppletViewer, a stand-alone tool for testing applets...
. - How Many Singles, Doubles, Triples, Etc., Should The Coupon Collector Expect?, a short note by Doron ZeilbergerDoron ZeilbergerDoron Zeilberger is an Israeli mathematician, known for his work in combinatorics.He is a Board of Governors Professor of Mathematics at Rutgers University...
.
- "Coupon Collector Problem" by Ed Pegg, Jr.
- Newman