
Cousin's theorem
Encyclopedia
In real analysis
, a branch of mathematics, Cousin's theorem states that:
This result was proved and established by Pierre Cousin, a student of Henri Poincaré
, in 1895, and it is an extension of the original Heine–Borel theorem
on compactness for arbitrary covers of any compact
subsets of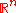 . However, Pierre Cousin did not receive any credit. Cousin's theorem was generally attributed to Henri Lebesgue
. However, Pierre Cousin did not receive any credit. Cousin's theorem was generally attributed to Henri Lebesgue
and renamed as Borel–Lebesgue theorem, who was aware of this result in 1898 and proved this in his dissertation in 1903.
Nowadays, it is stated as:
Further, Cousin's theorem is mainly only used in Henstock–Kurzweil integral and is often called Fineness Theorem or Cousin's lemma. It can be stated as:
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, a branch of mathematics, Cousin's theorem states that:
- If for every point of a closed region (in modern terms, "closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and bounded") there is a circle of finite radius (in modern term, a "neighborhoodNeighbourhood (mathematics)In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
") , then the region can be divided into a finite number of subregions such that each subregion is interior to a circle of a given set having its center in the subregion.
This result was proved and established by Pierre Cousin, a student of Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, in 1895, and it is an extension of the original Heine–Borel theorem
Heine–Borel theorem
In the topology of metric spaces the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:For a subset S of Euclidean space Rn, the following two statements are equivalent:*S is closed and bounded...
on compactness for arbitrary covers of any compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subsets of
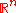 . However, Pierre Cousin did not receive any credit. Cousin's theorem was generally attributed to Henri Lebesgue
. However, Pierre Cousin did not receive any credit. Cousin's theorem was generally attributed to Henri LebesgueHenri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
and renamed as Borel–Lebesgue theorem, who was aware of this result in 1898 and proved this in his dissertation in 1903.
Nowadays, it is stated as:
- Let
 be a full cover of [a, b], that is, a collection of closed subintervals of [a, b] with the property that for every x∈[a, b], there exists a δ>0 so that
be a full cover of [a, b], that is, a collection of closed subintervals of [a, b] with the property that for every x∈[a, b], there exists a δ>0 so that  contains all subintervals of [a, b] which contains x and length smaller than δ. Then there exists a partition {I1, I2,...,In} of non-overlapping intervals for [a, b], where Ii=[xi-1, xi]∈
contains all subintervals of [a, b] which contains x and length smaller than δ. Then there exists a partition {I1, I2,...,In} of non-overlapping intervals for [a, b], where Ii=[xi-1, xi]∈ and a=x0 < x1 <...< xn=b for all 1≤i≤n.
and a=x0 < x1 <...< xn=b for all 1≤i≤n.
Further, Cousin's theorem is mainly only used in Henstock–Kurzweil integral and is often called Fineness Theorem or Cousin's lemma. It can be stated as:
- If I := [a, b] ⊆ Rn is a nondegenerateDegeneracy (mathematics)In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....
compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
interval and δ is any gauge defined on I, then there always exists a tagged partition of I that is δ-fine.

