Heine–Borel theorem
Encyclopedia
In the topology
of metric space
s the Heine–Borel theorem, named after Eduard Heine
and Émile Borel
, states:
For a subset
S of Euclidean space
Rn, the following two statements are equivalent:
In the context of real analysis
, the former property is sometimes used as the defining property of compactness. However, the two definitions cease to be equivalent when we consider subsets of more general metric space
s and in this generality only the latter property is used to define compactness. In fact, the Heine–Borel theorem for arbitrary metric spaces reads:
and the theorem stating that every continuous function
on a closed interval is uniformly continuous. Dirichlet was the first to prove this and implicitly he used the existence of a finite subcover of a given open cover of a closed interval in his proof. He used this proof in his 1862 lectures, which were published only in 1904. Later Eduard Heine
, Karl Weierstrass
and Salvatore Pincherle
used similar techniques. Émile Borel
in 1895 was the first to state and prove a form of what is now called the Heine–Borel theorem. His formulation was restricted to countable
covers. Pierre Cousin (1895), Lebesgue (1898) and Schoenflies (1900) generalized it to arbitrary covers.
Let S be a subset of Rn. Observe first the following: if a is a limit point
of S, then any finite collection C of open sets, such that each open set U ∈ C is disjoint from some neighborhood VU of a, fails to be a cover of S. Indeed, the intersection of the finite family of sets VU is a neighborhood W of a in Rn. Since a is a limit point of S, W must contain a point x in S. This x ∈ S is not covered by the family C, because every U in C is disjoint from VU and hence disjoint from W, which contains x.
If S is compact but not closed, then it has an accumulation point a not in S. Consider a collection consisting of an open neighborhood N(x) for each x ∈ S, chosen small enough to not intersect some neighborhood Vx of a. Then is an open cover of S, but any finite subcollection of has the form of C discussed previously, and thus cannot be an open subcover of S. This contradicts the compactness of S. Hence, every accumulation point of S is in S, so S is closed.
The proof above applies with almost no change to showing that any compact subset S of a Hausdorff
topological space X is closed in X.
If a set is compact, then it is bounded.
Consider the open balls centered upon a common point, with any radius. This can cover any set, because all points in the set are some distance away from that point. Any finite subcover of this cover must be bounded, because all balls in the subcover are contained in the largest open ball within that subcover. Therefore, any set covered by this subcover must also be bounded.
A closed subset of a compact set is compact.
Let K be a closed subset of a compact set T in Rn and let CK be an open cover of K. Then is an open set and
is an open cover of T. Since T is compact, then CT has a finite subcover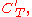
that also covers the smaller set K. Since U does not contain any point of K, the set K is already covered by 
that is a finite subcollection of the original collection CK. It is thus possible to extract from any open cover CK of K a finite subcover.
If a set is closed and bounded, then it is compact.
If a set S in Rn is bounded, then it can be enclosed within an n-box
where a > 0. By the property above, it is enough to show that T0 is compact.
Assume, by way of contradiction, that T0 is not compact. Then there exists an infinite open cover C of T0 that does not admit any finite subcover. Through bisection of each of the sides of T0, the box T0 can be broken up into 2n sub n-boxes, each of which has diameter equal to half the diameter of T0. Then at least one of the 2n sections of T0 must require an infinite subcover of C, otherwise C itself would have a finite subcover, by uniting together the finite covers of the sections. Call this section T1.
Likewise, the sides of T1 can be bisected, yielding 2n sections of T1, at least one of which must require an infinite subcover of C. Continuing in like manner yields a decreasing sequence of nested n-boxes:
where the side length of Tk is , which tends to 0 as k tends to infinity. Then, by Cantor's intersection theorem
, the infinite intersection
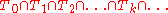
is not empty, but instead contains some point p ∈ T0. Since C covers T0, then it has some member U ∈ C such that p ∈ U. Since U is open, there is an n-ball . For large enough k, one has , but then the infinite number of members of C needed to cover Tk can be replaced by just one: U, a contradiction.
Thus, T0 is compact. Since S is closed and a subset of the compact set T0, then S is also compact (see above).
) is said to have the Heine–Borel property if every closed and bounded subset is compact. Many metric spaces fail to have the Heine–Borel property. For instance, the metric space of rational number
s (or indeed any incomplete metric space) fails to have the Heine–Borel property. Complete metric spaces may also fail to have the property. For instance, no infinite-dimensional Banach space
has the Heine–Borel property.
The theorem can be generalized to arbitrary metric spaces by strengthening the conditions required for compactness:
This generalisation also applies to topological vector space
s and, more generally, to uniform space
s.
Here is a sketch of the "
"-part of the proof, in the context of a general metric space, according to Jean Dieudonné
:
A proof of the "
"-part can be sketched as follows:
The proof of the "
" part easily generalises to arbitrary uniform spaces, but the proof of the "
" part is more complicated and is equivalent to the ultrafilter principle
, a weaker form of the Axiom of Choice. (Already, in general metric spaces, the "
" direction requires the
Axiom of dependent choice
.)
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s the Heine–Borel theorem, named after Eduard Heine
Eduard Heine
Heinrich Eduard Heine was a German mathematician.Heine became known for results on special functions and in real analysis. In particular, he authored an important treatise on spherical harmonics and Legendre functions . He also investigated basic hypergeometric series...
and Émile Borel
Émile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
, states:
For a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
S of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, the following two statements are equivalent:
- S is closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and boundedBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded... - every open cover of S has a finite subcover, that is, S is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
.
In the context of real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, the former property is sometimes used as the defining property of compactness. However, the two definitions cease to be equivalent when we consider subsets of more general metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s and in this generality only the latter property is used to define compactness. In fact, the Heine–Borel theorem for arbitrary metric spaces reads:
- A subset of a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is compact if and only if it is completeComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
and totally bounded.
History and motivation
The history of what today is called the Heine–Borel theorem starts in the 19th century, with the search for solid foundations of real analysis. Central to the theory was the concept of uniform continuityUniform continuity
In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
and the theorem stating that every continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on a closed interval is uniformly continuous. Dirichlet was the first to prove this and implicitly he used the existence of a finite subcover of a given open cover of a closed interval in his proof. He used this proof in his 1862 lectures, which were published only in 1904. Later Eduard Heine
Eduard Heine
Heinrich Eduard Heine was a German mathematician.Heine became known for results on special functions and in real analysis. In particular, he authored an important treatise on spherical harmonics and Legendre functions . He also investigated basic hypergeometric series...
, Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
and Salvatore Pincherle
Salvatore Pincherle
Salvatore Pincherle was an Italian mathematician. He contributed significantly to the field of functional analysis, established the Italian Mathematical Union , and was president of the Third International Congress of Mathematicians...
used similar techniques. Émile Borel
Émile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
in 1895 was the first to state and prove a form of what is now called the Heine–Borel theorem. His formulation was restricted to countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
covers. Pierre Cousin (1895), Lebesgue (1898) and Schoenflies (1900) generalized it to arbitrary covers.
Proof
If a set is compact, then it must be closed.Let S be a subset of Rn. Observe first the following: if a is a limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of S, then any finite collection C of open sets, such that each open set U ∈ C is disjoint from some neighborhood VU of a, fails to be a cover of S. Indeed, the intersection of the finite family of sets VU is a neighborhood W of a in Rn. Since a is a limit point of S, W must contain a point x in S. This x ∈ S is not covered by the family C, because every U in C is disjoint from VU and hence disjoint from W, which contains x.
If S is compact but not closed, then it has an accumulation point a not in S. Consider a collection consisting of an open neighborhood N(x) for each x ∈ S, chosen small enough to not intersect some neighborhood Vx of a. Then is an open cover of S, but any finite subcollection of has the form of C discussed previously, and thus cannot be an open subcover of S. This contradicts the compactness of S. Hence, every accumulation point of S is in S, so S is closed.
The proof above applies with almost no change to showing that any compact subset S of a Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological space X is closed in X.
If a set is compact, then it is bounded.
Consider the open balls centered upon a common point, with any radius. This can cover any set, because all points in the set are some distance away from that point. Any finite subcover of this cover must be bounded, because all balls in the subcover are contained in the largest open ball within that subcover. Therefore, any set covered by this subcover must also be bounded.
A closed subset of a compact set is compact.
Let K be a closed subset of a compact set T in Rn and let CK be an open cover of K. Then is an open set and
is an open cover of T. Since T is compact, then CT has a finite subcover
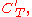that also covers the smaller set K. Since U does not contain any point of K, the set K is already covered by that is a finite subcollection of the original collection CK. It is thus possible to extract from any open cover CK of K a finite subcover.If a set is closed and bounded, then it is compact.
If a set S in Rn is bounded, then it can be enclosed within an n-box
where a > 0. By the property above, it is enough to show that T0 is compact.
Assume, by way of contradiction, that T0 is not compact. Then there exists an infinite open cover C of T0 that does not admit any finite subcover. Through bisection of each of the sides of T0, the box T0 can be broken up into 2n sub n-boxes, each of which has diameter equal to half the diameter of T0. Then at least one of the 2n sections of T0 must require an infinite subcover of C, otherwise C itself would have a finite subcover, by uniting together the finite covers of the sections. Call this section T1.
Likewise, the sides of T1 can be bisected, yielding 2n sections of T1, at least one of which must require an infinite subcover of C. Continuing in like manner yields a decreasing sequence of nested n-boxes:
where the side length of Tk is , which tends to 0 as k tends to infinity. Then, by Cantor's intersection theorem
Cantor's intersection theorem
In real analysis, a branch of mathematics, Cantor's intersection theorem, named after Georg Cantor, is a theorem related to compact sets in R, the set of real numbers. It states that a decreasing nested sequence of non-empty, closed and bounded subsets of R has nonempty intersection...
, the infinite intersection
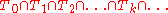
is not empty, but instead contains some point p ∈ T0. Since C covers T0, then it has some member U ∈ C such that p ∈ U. Since U is open, there is an n-ball . For large enough k, one has , but then the infinite number of members of C needed to cover Tk can be replaced by just one: U, a contradiction.
Thus, T0 is compact. Since S is closed and a subset of the compact set T0, then S is also compact (see above).
Generalizations
The theorem does not hold as stated for general metric spaces. A metric space (or topological vector spaceTopological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
) is said to have the Heine–Borel property if every closed and bounded subset is compact. Many metric spaces fail to have the Heine–Borel property. For instance, the metric space of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s (or indeed any incomplete metric space) fails to have the Heine–Borel property. Complete metric spaces may also fail to have the property. For instance, no infinite-dimensional Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
has the Heine–Borel property.
The theorem can be generalized to arbitrary metric spaces by strengthening the conditions required for compactness:
- A subset of a metric space is compact if and only if it is completeComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
and totally bounded.
This generalisation also applies to topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s and, more generally, to uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
s.
Here is a sketch of the "
"-part of the proof, in the context of a general metric space, according to Jean DieudonnéJean Dieudonné
Jean Alexandre Eugène Dieudonné was a French mathematician, notable for research in abstract algebra and functional analysis, for close involvement with the Nicolas Bourbaki pseudonymous group and the Éléments de géométrie algébrique project of Alexander Grothendieck, and as a historian of...
:
- It is obvious that any compact set E is totally bounded.
- Let (xn) be an arbitrary Cauchy sequenceCauchy sequenceIn mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
in E; let Fn be the closure of the set { xk : k ≥ n } in E and Un := E − Fn. If the intersection of all Fn were empty, (Un) would be an open cover of E, hence there would be a finite subcover (Unk) of E, hence the intersection of the Fnk would be empty; this implies that Fn is empty for all n larger than any of the nk, which is a contradiction. Hence, the intersection of all Fn is not empty, and any point in this intersection is an accumulation point of the sequence (xn). - Any accumulation point of a Cauchy sequence is a limit point (xn); hence any Cauchy sequence in E converges in E, in other words: E is complete.
A proof of the "
"-part can be sketched as follows:
- If E were not compact, there would exist a cover (Ul)l of E having no finite subcover of E. Use the total boundedness of E to define inductively a sequence of balls (Bn) in E with
- the radius of Bn is 2−n;
- there is no finite subcover (Ul∩Bn)l of Bn;
- Bn+1 ∩ Bn is not empty.
- Let xn be the center point of Bn and let yn be any point in Bn+1 ∩ Bn; hence we have d(xn+1, xn) ≤ d(xn+1, yn) + d(yn, xn) ≤ 2−n−1 + 2−n ≤ 2−n+1. It follows for n ≤ p < q: d(xp, xq) ≤ d(xp, xp+1) + ... + d(xq−1, xq) ≤ 2−p+1 + ... + 2−q+2 ≤ 2−n+2. Therefore, (xn) is a Cauchy sequence in E, converging to some limit point a in E, because E is complete.
- Let
be an index such that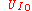 
contains a; since (xn) converges to a and 
is open, there is a large n such that the ball Bn is a subset of 
–v in contradiction to the construction of Bn.
The proof of the "
" part easily generalises to arbitrary uniform spaces, but the proof of the "" part is more complicated and is equivalent to the ultrafilter principleBoolean prime ideal theorem
In mathematics, a prime ideal theorem guarantees the existence of certain types of subsets in a given abstract algebra. A common example is the Boolean prime ideal theorem, which states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on...
, a weaker form of the Axiom of Choice. (Already, in general metric spaces, the "
" direction requires theAxiom of dependent choice
Axiom of dependent choice
In mathematics, the axiom of dependent choices, denoted DC, is a weak form of the axiom of choice which is still sufficient to develop most of real analysis...
.)