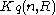Covering code
Encyclopedia
In coding theory
, a covering code is an object satisfying a certain mathematical property: A code of length n over Q is an R-covering code if for every word of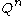 there is a codeword such that their Hamming distance
there is a codeword such that their Hamming distance
is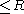 .
.
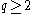 ,
, 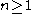 ,
, 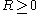 be integers.
be integers.
A code
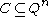 over an alphabet
over an alphabet
Q of size |Q| = q is called
q-ary R-covering code of length n
if for every word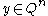 there is a codeword
there is a codeword 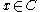
such that the Hamming distance
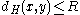 .
.
In other words, the spheres
(or balls or rook
-domains) of radius
R
with respect to the Hamming metric
around the codewords of C have to exhaust
the finite metric space
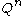 .
.
The covering radius of a code C is the smallest R such that C is R-covering.
Every perfect code is a covering code of minimal size.
of the minimal size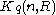 of a q-ary R-covering code of length n is a very hard problem. In many cases, only lower and upper bounds are known with a large gap between them.
of a q-ary R-covering code of length n is a very hard problem. In many cases, only lower and upper bounds are known with a large gap between them.
Every construction of a covering code gives an upper bound on Kq(n, R).
Lower bounds include the sphere covering bound and
Rodemich’s bounds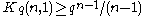 and
and 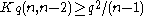 .
.
The covering problem is closely related to the packing problem in , i.e. the determination of the maximal size of a q-ary e-error correcting
, i.e. the determination of the maximal size of a q-ary e-error correcting
code of length n.
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, a covering code is an object satisfying a certain mathematical property: A code of length n over Q is an R-covering code if for every word of
 there is a codeword such that their Hamming distance
there is a codeword such that their Hamming distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
is
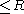 .
.Definition
Let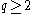 ,
, 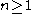 ,
, 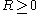 be integers.
be integers.A code
Code
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
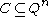 over an alphabet
over an alphabetAlphabet
An alphabet is a standard set of letters—basic written symbols or graphemes—each of which represents a phoneme in a spoken language, either as it exists now or as it was in the past. There are other systems, such as logographies, in which each character represents a word, morpheme, or semantic...
Q of size |Q| = q is called
q-ary R-covering code of length n
if for every word
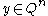 there is a codeword
there is a codeword 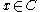
such that the Hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
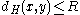 .
.In other words, the spheres
SPHERES
The Synchronized Position Hold, Engage, Reorient Experimental Satellites experiment is a testbed consisting of three miniaturized satellites that can operate in a variety of environments, including inside the International Space Station...
(or balls or rook
Rook
-Games:*Rook or castle, a piece in the board game of chess*Rook , a trick-taking game, usually played with a specialized deck of cards-People:*Alan Rook, editor of the 1936 issue of New Oxford Poetry, one of the Cairo poets...
-domains) of radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
R
with respect to the Hamming metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
around the codewords of C have to exhaust
the finite metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
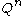 .
.The covering radius of a code C is the smallest R such that C is R-covering.
Every perfect code is a covering code of minimal size.
Example
C = {0134,0223,1402,1431,1444,2123,2234,3002,3310,4010,4341} is a 5-ary 2-covering code of length 4.Covering problem
The determinationDetermination
Determination may refer to:* Determination , 2001* Determination , 1992* Cell fate determination* Co-determination* Coefficient of determination* Expert determination* Hidden surface determination...
of the minimal size
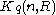 of a q-ary R-covering code of length n is a very hard problem. In many cases, only lower and upper bounds are known with a large gap between them.
of a q-ary R-covering code of length n is a very hard problem. In many cases, only lower and upper bounds are known with a large gap between them.Every construction of a covering code gives an upper bound on Kq(n, R).
Lower bounds include the sphere covering bound and
Rodemich’s bounds
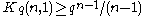 and
and 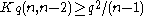 .
.The covering problem is closely related to the packing problem in
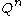 , i.e. the determination of the maximal size of a q-ary e-error correcting
, i.e. the determination of the maximal size of a q-ary e-error correctingError detection and correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction or error control are techniques that enable reliable delivery of digital data over unreliable communication channels...
code of length n.
Applications
The standard work on covering codes lists the following applications.- Compression with distortionDistortionA distortion is the alteration of the original shape of an object, image, sound, waveform or other form of information or representation. Distortion is usually unwanted, and often many methods are employed to minimize it in practice...
- Data compressionData compressionIn computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
- DecodingDecodingDecoding is the reverse of encoding, which is the process of transforming information from one format into another. Information about decoding can be found in the following:* Digital-to-analog converter, the use of analog circuit for decoding operations...
errors and erasures - BroadcastingBroadcastingBroadcasting is the distribution of audio and video content to a dispersed audience via any audio visual medium. Receiving parties may include the general public or a relatively large subset of thereof...
in interconnection networks - Football poolsFootball poolsA football pool, often collectively referred to as "the pools", is a betting pool based on predicting the outcome of top-level association football matches set to take place in the coming week. The pools are typically cheap to enter, with the potential to win huge money. Entries were traditionally...
- Write-once memories
- Berlekamp-Gale game
- Speech codingSpeech codingSpeech coding is the application of data compression of digital audio signals containing speech. Speech coding uses speech-specific parameter estimation using audio signal processing techniques to model the speech signal, combined with generic data compression algorithms to represent the resulting...
- Cellular telecommunications
- SubsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
sums and Cayley graphCayley graphIn mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
s