
Covering system
Encyclopedia
In mathematics
, a covering system (also called a complete residue system) is a collection
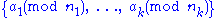
of finitely many
residue classes
whose union covers all the integers.
in the early 1930s.
The following are examples of covering systems:
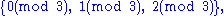
and
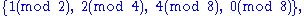
and
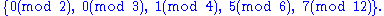
A covering system is called disjoint (or exact) if no two members overlap.
A covering system is called distinct (or incongruent) if all the moduli are different (and bigger than 1).
A covering system is called irredundant (or minimal) if all the residue classes are required to cover the integers.
The first two examples are disjoint.
The third example is distinct.
A system (i.e., an unordered multi-set)
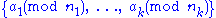
of finitely many
residue classes is called an -cover if it covers every integer at least
-cover if it covers every integer at least
 times, and an exact
times, and an exact  -cover if it covers each integer exactly
-cover if it covers each integer exactly  times. It is known that for each
times. It is known that for each
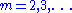 there are exact
there are exact  -covers which cannot be written as a union of two covers. For example,
-covers which cannot be written as a union of two covers. For example,

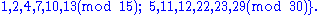
is an exact 2-cover which is not a union of two covers.
is unsolved: Whether for any arbitrarily large N there exists an incongruent covering system the minimum of whose moduli is at least N. It is easy to construct examples where the minimum of the moduli in such a system is 2, or 3 (Erdős gave an example where the moduli are in the set of the divisors of 120; a suitable cover is 0(3), 0(4), 0(5), 1(6), 1(8), 2(10), 11(12), 1(15), 14(20), 5(24), 8(30), 6(40), 58(60), 26(120) ); D. Swift gave an example where the minimum of the moduli is 4 (and the moduli are in the set of the divisors of 2880). S. L. G. Choi proved that it is possible to give an example for N = 20, and Pace P Nielsen demonstrates the existence of an example with N = 40, consisting of more than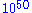 congruences.
congruences.
In another problem we want that all of the moduli (of an incongruent covering system) be odd. There is a famous unsolved conjecture from Erdős and Selfridge: an incongruent covering system (with the minimum modulus greater than 1) whose moduli are odd, does not exist. It is known that if such a system exists, the overall modulus must have at least 22 prime factors.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a covering system (also called a complete residue system) is a collection
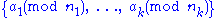
of finitely many
residue classes

whose union covers all the integers.
Examples and definitions
The notion of covering system was introduced by Paul ErdősPaul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
in the early 1930s.
The following are examples of covering systems:
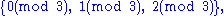
and
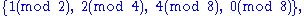
and
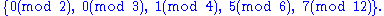
A covering system is called disjoint (or exact) if no two members overlap.
A covering system is called distinct (or incongruent) if all the moduli are different (and bigger than 1).
A covering system is called irredundant (or minimal) if all the residue classes are required to cover the integers.
The first two examples are disjoint.
The third example is distinct.
A system (i.e., an unordered multi-set)
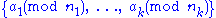
of finitely many
residue classes is called an
 -cover if it covers every integer at least
-cover if it covers every integer at least times, and an exact
times, and an exact  -cover if it covers each integer exactly
-cover if it covers each integer exactly  times. It is known that for each
times. It is known that for each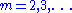 there are exact
there are exact  -covers which cannot be written as a union of two covers. For example,
-covers which cannot be written as a union of two covers. For example,
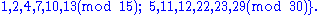
is an exact 2-cover which is not a union of two covers.
Some unsolved problems
The following problem from Paul ErdősPaul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
is unsolved: Whether for any arbitrarily large N there exists an incongruent covering system the minimum of whose moduli is at least N. It is easy to construct examples where the minimum of the moduli in such a system is 2, or 3 (Erdős gave an example where the moduli are in the set of the divisors of 120; a suitable cover is 0(3), 0(4), 0(5), 1(6), 1(8), 2(10), 11(12), 1(15), 14(20), 5(24), 8(30), 6(40), 58(60), 26(120) ); D. Swift gave an example where the minimum of the moduli is 4 (and the moduli are in the set of the divisors of 2880). S. L. G. Choi proved that it is possible to give an example for N = 20, and Pace P Nielsen demonstrates the existence of an example with N = 40, consisting of more than
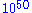 congruences.
congruences.In another problem we want that all of the moduli (of an incongruent covering system) be odd. There is a famous unsolved conjecture from Erdős and Selfridge: an incongruent covering system (with the minimum modulus greater than 1) whose moduli are odd, does not exist. It is known that if such a system exists, the overall modulus must have at least 22 prime factors.
See also
- Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
- Covering setCovering setIn mathematics, a covering set for a sequence of integers refers to a set of prime numbers such that every term in the sequence is divisible by at least one member of the set...
- Residue number systemResidue number systemA residue number system represents a large integer using a set of smaller integers, so that computation may be performed more efficiently...
- Herzog–Schönheim conjecture
External links
- Zhi-Wei SunZhi-Wei SunZhi-Wei Sun is a Chinese mathematician, working primarily on number theory, combinatorics, and group theory. Currently he works as a professor in Nanjing University....
: Problems and Results on Covering Systems (a survey) (PDF) - Zhi-Wei Sun: Classified Publications on Covering Systems (PDF)

