Residue number system
Encyclopedia
A residue number system represents a large integer using a set of smaller integers, so that computation
may be performed more efficiently. It relies on the Chinese remainder theorem
of modular arithmetic
for its operation, a mathematical idea from Sun Tsu Suan-Ching
(Master Sun’s Arithmetic Manual) in the 4th century AD.
referred to as the moduli. Let M be the least common multiple
of all the mi.
Any arbitrary integer X smaller than M can be represented in the defined residue number system as a set of N smaller integers
with
representing the residue class of X to that modulus.
Note that for maximum representational efficiency it is imperative that all the moduli are coprime
; that is, no modulus may have a common factor with any other. M is then the product of all the mi.
For example RNS(4|2) has non-coprime moduli, resulting in the same representation for different values.
(3)decimal = (3|1)RNS(4|2)
(7)decimal = (3|1)RNS(4|2)
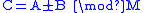
can be calculated in RNS as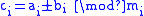
One has to check for overflow
in these operations.
we can calculate: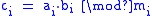
Again overflows are possible.
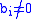) then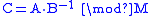
can be easily calculated by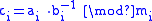
where
is multiplicative inverse
of B modulo M, and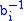
is multiplicative inverse of 
modulo 
.
computer arithmetic. By decomposing in this a large integer into a set of smaller integers, a large calculation can be performed as a series of smaller calculations that can be performed independently and in parallel. Because of this, it's particularly popular in hardware implementations.
. Let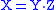
a semiprime
. Let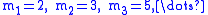
represent first N primes. Assume that 
, 
. Then 
, where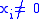 
. The method of trial division is the method of exhaustion, and the RNS automatically eliminates all Y and Z such that 
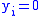or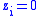 
, that is we only need to check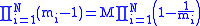
numbers below M. For example, N = 3, the RNS can automatically eliminate all numbers but
or 73% of numbers. For N = 25 when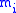
are all prime numbers below 100, the RNS eliminates about 88% of numbers. One can see from the above formula the diminishing returns from the larger sets of moduli.
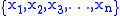in the RNS can be naturally represented in the associated mixed radix
system (AMRS)
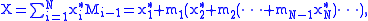
where
for 
and 
Note that after conversion from the RNS to AMRS, the comparison of numbers becomes straightforward.
Computation
Computation is defined as any type of calculation. Also defined as use of computer technology in Information processing.Computation is a process following a well-defined model understood and expressed in an algorithm, protocol, network topology, etc...
may be performed more efficiently. It relies on the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
of modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
for its operation, a mathematical idea from Sun Tsu Suan-Ching
Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
(Master Sun’s Arithmetic Manual) in the 4th century AD.
Defining a residue number system
A residue number system is defined by a set of N integer constants,- {m1, m2, m3, ... , mN },
referred to as the moduli. Let M be the least common multiple
Least common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
of all the mi.
Any arbitrary integer X smaller than M can be represented in the defined residue number system as a set of N smaller integers
- {x1, x2, x3, ... , xN}
with
- xi = X moduloModulo operationIn computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
mi
representing the residue class of X to that modulus.
Note that for maximum representational efficiency it is imperative that all the moduli are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
; that is, no modulus may have a common factor with any other. M is then the product of all the mi.
For example RNS(4|2) has non-coprime moduli, resulting in the same representation for different values.
(3)decimal = (3|1)RNS(4|2)
(7)decimal = (3|1)RNS(4|2)
Operations on RNS numbers
Once represented in RNS, many arithmetic operations can be efficiently performed on the encoded integer. For the following operations, consider two integers, A and B, represented by ai and bi in an RNS system defined by mi (for i from 0 ≤ i ≤ N).Addition and subtraction
Addition (or subtraction) can be accomplished by simply adding (or subtracting) the small integer values, modulo their specific moduli. That is,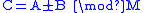can be calculated in RNS as
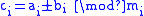
One has to check for overflow
Arithmetic overflow
The term arithmetic overflow or simply overflow has the following meanings.# In a computer, the condition that occurs when a calculation produces a result that is greater in magnitude than that which a given register or storage location can store or represent.# In a computer, the amount by which a...
in these operations.
Multiplication
Multiplication can be accomplished in a manner similar to addition and subtraction. To calculatewe can calculate:
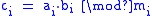
Again overflows are possible.
Division
Division in residue number systems is problematic. A paper describing one possible algorithm is available at http://www.cs.rpi.edu/research/ps/93-9.ps. On the other hand, if B is coprime with M (that is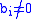) then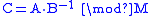can be easily calculated by
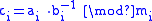
where
is multiplicative inverseMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of B modulo M, and
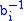is multiplicative inverse of modulo .Practical applications
RNS have applications in the field of digitalDigital
A digital system is a data technology that uses discrete values. By contrast, non-digital systems use a continuous range of values to represent information...
computer arithmetic. By decomposing in this a large integer into a set of smaller integers, a large calculation can be performed as a series of smaller calculations that can be performed independently and in parallel. Because of this, it's particularly popular in hardware implementations.
Integer factorization
The RNS can improve efficiency of trial divisionTrial division
Trial division is the most laborious but easiest to understand of the integer factorization algorithms. Its ease of implementation makes it a viable integer factorization option for devices with little available memory, such as graphing calculators....
. Let
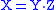a semiprimeSemiprime
In mathematics, a semiprime is a natural number that is the product of two prime numbers. The first few semiprimes are 4, 6, 9, 10, 14, 15, 21, 22, 25, 26, ... ....
. Let
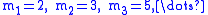represent first N primes. Assume that , . Then , where 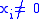. The method of trial division is the method of exhaustion, and the RNS automatically eliminates all Y and Z such that 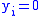or 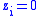, that is we only need to check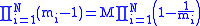numbers below M. For example, N = 3, the RNS can automatically eliminate all numbers but
- 1,7,11,13,17,19,23,29 mod 30
or 73% of numbers. For N = 25 when
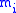are all prime numbers below 100, the RNS eliminates about 88% of numbers. One can see from the above formula the diminishing returns from the larger sets of moduli.Associated mixed radix system
A number given by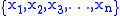 in the RNS can be naturally represented in the associated mixed radixMixed radix
Mixed radix numeral systems are non-standard positional numeral systems in which the numerical base varies from position to position. Such numerical representation applies when a quantity is expressed using a sequence of units that are each a multiple of the next smaller one, but not by the same...
system (AMRS)
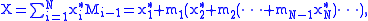
where
for and Note that after conversion from the RNS to AMRS, the comparison of numbers becomes straightforward.