Custodial symmetry
Encyclopedia
In particle physics
with one or more electroweak Higgs doublets in the Higgs sector
, the effective action
term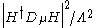
which generically arises whenever we have new physics beyond the Standard Model
at the scale Λ contributes to the Peskin-Takeuchi T parameter. However, current precision electroweak measurements restrict Λ to more than a few TeV
. This will not be a problem if we have no new physics right up to at least that scale. However, attempts to solve the gauge hierarchy problem generically require the addition of new particles below that scale. The preferred way of preventing the nasty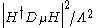
term from being generated is to introduce an approximate symmetry which acts upon the Higgs sector. In addition to the gauged SU(2)W which acts exactly upon the Higgs doublets, we will also introduce another approximate global SU(2)R symmetry which also acts upon the Higgs doublet. The Higgs doublet is now a real representation
(2,2) of SU(2)L × SU(2)R with four real components. Here, we have relabeled W as L following the standard convention. Such a symmetry will not forbid Higgs kinetic terms like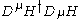
or tachyonic mass terms like 
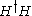or self-coupling terms like 
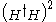(fortunately!) but will outlaw 
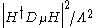. On the other hand, such an SU(2)R symmetry can never be exact and unbroken because otherwise, the up-type and the down-type Yukawa couplings will be exactly identical. Besides, SU(2)R does not map the hypercharge
symmetry U(1)Y to itself but this is not too much of a problem because the hypercharge gauge coupling strength is small and in the limit as it goes to zero, we won't have a problem. In the parlance of model building, we say that U(1)Y is weakly gauged and this explicitly breaks SU(2)R. After the Higgs doublet acquires a nonzero vacuum expectation value
, the (approximate) SU(2)L × SU(2)R symmetry is spontaneously broken to the (approximate) diagonal subgroup SU(2)V. This approximate symmetry is called the custodial symmetry.
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
with one or more electroweak Higgs doublets in the Higgs sector
Higgs sector
In particle physics, the Higgs sector is the collection of quantum fields and/or particles that are responsible for the Higgs mechanism i.e. for the spontaneous symmetry breaking. The word "sector" refers to a subgroup of the total set of fields and particles...
, the effective action
Effective action
In quantum field theory, the effective action is a modified expression for the action, which takes into account quantum-mechanical corrections, in the following sense:...
term
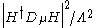which generically arises whenever we have new physics beyond the Standard ModelBeyond the Standard Model
Physics beyond the Standard Model refers to the theoretical developments needed to explain the deficiencies of the Standard Model, such as the origin of mass, the strong CP problem, neutrino oscillations, matter–antimatter asymmetry, and the nature of dark matter and dark energy...
at the scale Λ contributes to the Peskin-Takeuchi T parameter. However, current precision electroweak measurements restrict Λ to more than a few TeV
TEV
TEV may refer to:* TeV, or teraelectronvolt, a measure of energy* Total Enterprise Value, a financial measure* Total Economic Value, an economic measure* Tobacco etch virus, a plant pathogenic virus of the family Potyviridae....
. This will not be a problem if we have no new physics right up to at least that scale. However, attempts to solve the gauge hierarchy problem generically require the addition of new particles below that scale. The preferred way of preventing the nasty
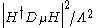term from being generated is to introduce an approximate symmetry which acts upon the Higgs sector. In addition to the gauged SU(2)W which acts exactly upon the Higgs doublets, we will also introduce another approximate global SU(2)R symmetry which also acts upon the Higgs doublet. The Higgs doublet is now a real representationReal representation
In the mathematical field of representation theory a real representation is usually a representation on a real vector space U, but it can also mean a representation on a complex vector space V with an invariant real structure, i.e., an antilinear equivariant mapj\colon V\to V\,which...
(2,2) of SU(2)L × SU(2)R with four real components. Here, we have relabeled W as L following the standard convention. Such a symmetry will not forbid Higgs kinetic terms like
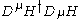or tachyonic mass terms like 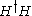or self-coupling terms like 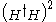(fortunately!) but will outlaw 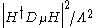. On the other hand, such an SU(2)R symmetry can never be exact and unbroken because otherwise, the up-type and the down-type Yukawa couplings will be exactly identical. Besides, SU(2)R does not map the hyperchargeHypercharge
In particle physics, the hypercharge Y of a particle is related to the strong interaction, and is distinct from the similarly named weak hypercharge, which has an analogous role in the electroweak interaction...
symmetry U(1)Y to itself but this is not too much of a problem because the hypercharge gauge coupling strength is small and in the limit as it goes to zero, we won't have a problem. In the parlance of model building, we say that U(1)Y is weakly gauged and this explicitly breaks SU(2)R. After the Higgs doublet acquires a nonzero vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
, the (approximate) SU(2)L × SU(2)R symmetry is spontaneously broken to the (approximate) diagonal subgroup SU(2)V. This approximate symmetry is called the custodial symmetry.