
D-ary heap
Encyclopedia
The -ary heap or -heap is a priority queue
data structure
, a generalization of the binary heap
in which the nodes have children instead of 2. Thus, a binary heap is a 2-heap. According to Tarjan and Jensen et al., -ary heaps were invented by Donald B. Johnson
in 1975.
This data structure allows decrease priority operations to be performed more quickly than binary heaps, at the expense of slower delete minimum operations. This tradeoff leads to better running times for algorithms such as Dijkstra's algorithm
in which decrease priority operations are more common than delete min operations. Additionally, -ary heaps have better memory cache behavior than a binary heap, allowing them to run more quickly in practice despite having a theoretically larger worst-case running time. Like binary heaps, -ary heaps are an in-place data structure
that uses no additional storage beyond that needed to store the array of items in the heap.
: the item at position 0 of the array forms the root of the tree, the items at positions 1– are its children, the next items are its grandchildren, etc. Thus, the parent of the item at position (for any ) is the item at position and its children are the items at positions through . According to the heap property
, in a min-heap, each item has a priority that is at least as large as its parent; in a max-heap, each item has a priority that is no larger than its parent.
The minimum priority item in a min-heap (or the maximum priority item in a max-heap) may always be found at position 0 of the array. To remove this item from the priority queue, the last item x in the array is moved into its place, and the length of the array is decreased by one. Then, while item x and its children do not satisfy the heap property, item x is swapped with one of its children (the one with the smallest priority in a min-heap, or the one with the largest priority in a max-heap), moving it downward in the tree and later in the array, until eventually the heap property is satisfied. The same downward swapping procedure may be used to increase the priority of an item in a min-heap, or to decrease the priority of an item in a max-heap.
To insert a new item into the heap, the item is appended to the end of the array, and then while the heap property is violated it is swapped with its parent, moving it upward in the tree and earlier in the array, until eventually the heap property is satisfied. The same upward-swapping procedure may be used to decrease the priority of an item in a min-heap, or to increase the priority of an item in a max-heap.
To create a new heap from an array of items, one may loop over the items in reverse order, starting from the item at position and ending at the item at position 0, applying the downward-swapping procedure for each item.
When creating a -ary heap from a set of n items, most of the items are in positions that will eventually hold leaves of the -ary tree, and no downward swapping is performed for those items. At most items are non-leaves, and may be swapped downwards at least once, at a cost of time to find the child to swap them with. At most nodes may be swapped downward two times, incurring an additional cost for the second swap beyond the cost already counted in the first term, etc. Therefore, the total amount of time to create a heap in this way is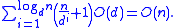
The space usage of the heap, with insert and delete-min operations, is linear, as it uses no extra storage other than an array containing a list of the items in the heap. If changes to the priorities of existing items need to be supported, then one must also maintain pointers from the items to their positions in the heap, which again uses only linear storage.
for shortest paths in graphs and Prim's algorithm
for minimum spanning tree
s both use a min-heap in which there are delete-min operations and as many as decrease-priority operations, where is the number of vertices in the graph and m is the number of edges. By using a -ary heap with , the total times for these two types of operations may be balanced against each other, leading to a total time of for the algorithm, an improvement over the running time of binary heap versions of these algorithms whenever the number of edges is significantly larger than the number of vertices. An alternative priority queue data structure, the Fibonacci heap
, gives an even better theoretical running time of , but in practice -ary heaps are generally at least as fast, and often faster, than Fibonacci heaps for this application.
4-heaps may perform better than binary heaps in practice, even for delete-min operations. Additionally,
a -ary heap typically runs much faster than a binary heap for heap sizes that exceed the size of the computer's cache memory:
A binary heap typically requires more cache misses and virtual memory
page fault
s than a -ary heap, each one taking far more time than the extra work incurred by the additional comparisons a -ary heap makes compared to a binary heap.
Priority queue
A priority queue is an abstract data type in computer programming.It is exactly like a regular queue or stack data structure, but additionally, each element is associated with a "priority"....
data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
, a generalization of the binary heap
Binary heap
A binary heap is a heap data structure created using a binary tree. It can be seen as a binary tree with two additional constraints:*The shape property: the tree is a complete binary tree; that is, all levels of the tree, except possibly the last one are fully filled, and, if the last level of...
in which the nodes have children instead of 2. Thus, a binary heap is a 2-heap. According to Tarjan and Jensen et al., -ary heaps were invented by Donald B. Johnson
Donald B. Johnson
Donald Bruce Johnson was an American computer scientist, a researcher in the design and analysis of algorithms, and the founding chair of the computer science department at Dartmouth College....
in 1975.
This data structure allows decrease priority operations to be performed more quickly than binary heaps, at the expense of slower delete minimum operations. This tradeoff leads to better running times for algorithms such as Dijkstra's algorithm
Dijkstra's algorithm
Dijkstra's algorithm, conceived by Dutch computer scientist Edsger Dijkstra in 1956 and published in 1959, is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree...
in which decrease priority operations are more common than delete min operations. Additionally, -ary heaps have better memory cache behavior than a binary heap, allowing them to run more quickly in practice despite having a theoretically larger worst-case running time. Like binary heaps, -ary heaps are an in-place data structure
In-place algorithm
In computer science, an in-place algorithm is an algorithm which transforms input using a data structure with a small, constant amount of extra storage space. The input is usually overwritten by the output as the algorithm executes...
that uses no additional storage beyond that needed to store the array of items in the heap.
Data structure
The -ary heap consists of an array of items, each of which has a priority associated with it. These items may be viewed as the nodes in a complete -ary tree, listed in breadth first traversal orderBreadth-first search
In graph theory, breadth-first search is a graph search algorithm that begins at the root node and explores all the neighboring nodes...
: the item at position 0 of the array forms the root of the tree, the items at positions 1– are its children, the next items are its grandchildren, etc. Thus, the parent of the item at position (for any ) is the item at position and its children are the items at positions through . According to the heap property
Binary heap
A binary heap is a heap data structure created using a binary tree. It can be seen as a binary tree with two additional constraints:*The shape property: the tree is a complete binary tree; that is, all levels of the tree, except possibly the last one are fully filled, and, if the last level of...
, in a min-heap, each item has a priority that is at least as large as its parent; in a max-heap, each item has a priority that is no larger than its parent.
The minimum priority item in a min-heap (or the maximum priority item in a max-heap) may always be found at position 0 of the array. To remove this item from the priority queue, the last item x in the array is moved into its place, and the length of the array is decreased by one. Then, while item x and its children do not satisfy the heap property, item x is swapped with one of its children (the one with the smallest priority in a min-heap, or the one with the largest priority in a max-heap), moving it downward in the tree and later in the array, until eventually the heap property is satisfied. The same downward swapping procedure may be used to increase the priority of an item in a min-heap, or to decrease the priority of an item in a max-heap.
To insert a new item into the heap, the item is appended to the end of the array, and then while the heap property is violated it is swapped with its parent, moving it upward in the tree and earlier in the array, until eventually the heap property is satisfied. The same upward-swapping procedure may be used to decrease the priority of an item in a min-heap, or to increase the priority of an item in a max-heap.
To create a new heap from an array of items, one may loop over the items in reverse order, starting from the item at position and ending at the item at position 0, applying the downward-swapping procedure for each item.
Analysis
In a -ary heap with items in it, both the upward-swapping procedure and the downward-swapping procedure may perform as many as swaps. In the upward-swapping procedure, each swap involves a single comparison of an item with its parent, and takes constant time. Therefore, the time to insert a new item into the heap, to decrease the priority of an item in a min-heap, or to increase the priority of an item in a max-heap, is . In the downward-swapping procedure, each swap involves comparisons and takes time: it takes comparisons to determine the minimum or maximum of the children and then one more comparison against the parent to determine whether a swap is needed. Therefore, the time to delete the root item, to increase the priority of an item in a min-heap, or to decrease the priority of an item in a max-heap, is .When creating a -ary heap from a set of n items, most of the items are in positions that will eventually hold leaves of the -ary tree, and no downward swapping is performed for those items. At most items are non-leaves, and may be swapped downwards at least once, at a cost of time to find the child to swap them with. At most nodes may be swapped downward two times, incurring an additional cost for the second swap beyond the cost already counted in the first term, etc. Therefore, the total amount of time to create a heap in this way is
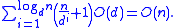
The space usage of the heap, with insert and delete-min operations, is linear, as it uses no extra storage other than an array containing a list of the items in the heap. If changes to the priorities of existing items need to be supported, then one must also maintain pointers from the items to their positions in the heap, which again uses only linear storage.
Applications
Dijkstra's algorithmDijkstra's algorithm
Dijkstra's algorithm, conceived by Dutch computer scientist Edsger Dijkstra in 1956 and published in 1959, is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree...
for shortest paths in graphs and Prim's algorithm
Prim's algorithm
In computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
for minimum spanning tree
Minimum spanning tree
Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...
s both use a min-heap in which there are delete-min operations and as many as decrease-priority operations, where is the number of vertices in the graph and m is the number of edges. By using a -ary heap with , the total times for these two types of operations may be balanced against each other, leading to a total time of for the algorithm, an improvement over the running time of binary heap versions of these algorithms whenever the number of edges is significantly larger than the number of vertices. An alternative priority queue data structure, the Fibonacci heap
Fibonacci heap
In computer science, a Fibonacci heap is a heap data structure consisting of a collection of trees. It has a better amortized running time than a binomial heap. Fibonacci heaps were developed by Michael L. Fredman and Robert E. Tarjan in 1984 and first published in a scientific journal in 1987...
, gives an even better theoretical running time of , but in practice -ary heaps are generally at least as fast, and often faster, than Fibonacci heaps for this application.
4-heaps may perform better than binary heaps in practice, even for delete-min operations. Additionally,
a -ary heap typically runs much faster than a binary heap for heap sizes that exceed the size of the computer's cache memory:
A binary heap typically requires more cache misses and virtual memory
Virtual memory
In computing, virtual memory is a memory management technique developed for multitasking kernels. This technique virtualizes a computer architecture's various forms of computer data storage , allowing a program to be designed as though there is only one kind of memory, "virtual" memory, which...
page fault
Page fault
A page fault is a trap to the software raised by the hardware when a program accesses a page that is mapped in the virtual address space, but not loaded in physical memory. In the typical case the operating system tries to handle the page fault by making the required page accessible at a location...
s than a -ary heap, each one taking far more time than the extra work incurred by the additional comparisons a -ary heap makes compared to a binary heap.

