
Darboux's theorem (analysis)
Encyclopedia
Darboux's theorem is a theorem
in real analysis
, named after Jean Gaston Darboux
. It states that all functions that result from the differentiation
of other functions have the intermediate value property: the image
of an interval
is also an interval.
When f is continuously
differentiable (f in C1([a,b])), this is a consequence of the intermediate value theorem
. But even when f′ is not continuous, Darboux's theorem places a severe restriction on what it can be.
on [a,b], which is differentiable
on (a,b), differentiable from the right at a, and differentiable from the left at b. Then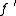 satisfies the intermediate value property: for every t between
satisfies the intermediate value property: for every t between 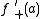 and
and 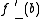 , there is some x in [a,b] such that
, there is some x in [a,b] such that 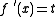 .
.
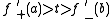 . Let
. Let 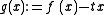 . Then
. Then  exists by hypothesis,
exists by hypothesis, 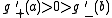 , and we wish to find a zero of
, and we wish to find a zero of  .
.
By hypothesis, g is a continuous function on [a,b], by the extreme value theorem
it attains a maximum on [a,b]. This maximum cannot be at a, since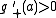 so there should be a point
so there should be a point 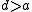 with
with 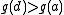 . Similarly,
. Similarly, 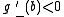 , so g cannot have a maximum at b. So the maximum is attained at some c in (a,b). But then
, so g cannot have a maximum at b. So the maximum is attained at some c in (a,b). But then 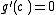 by Fermat's theorem (stationary points)
by Fermat's theorem (stationary points)
.
f which has the "intermediate value property": for any two values a and b in the domain of f, and any y between f(a) and f(b), there is some c between a and b with f(c) = y. By the intermediate value theorem
, every continuous function
is a Darboux function. Darboux's contribution was to show that there are discontinuous Darboux functions.
Every discontinuity of a Darboux function is essential, that is, at any point of discontinuity, at least one of the left hand and right hand limits does not exist.
An example of a Darboux function that is discontinuous at one point, is the function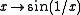 .
.
As a consequence of the mean value theorem
, the derivative of any differentiable function is a Darboux function. In particular, the derivative of the function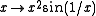 is a Darboux function that is not continuous.
is a Darboux function that is not continuous.
An example of a Darboux function that is nowhere continuous is the Conway base 13 function
.
Darboux functions are a quite general class of functions. It turns out that any real-valued function f on the real line can be written as the sum of two Darboux functions. This implies in particular that the class of Darboux functions is not closed under addition.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, named after Jean Gaston Darboux
Jean Gaston Darboux
Jean-Gaston Darboux was a French mathematician.-Life:Darboux made several important contributions to geometry and mathematical analysis . He was a biographer of Henri Poincaré and he edited the Selected Works of Joseph Fourier.Darboux received his Ph.D...
. It states that all functions that result from the differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of other functions have the intermediate value property: the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
is also an interval.
When f is continuously
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
differentiable (f in C1([a,b])), this is a consequence of the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
. But even when f′ is not continuous, Darboux's theorem places a severe restriction on what it can be.
Darboux's theorem
Let f : [a,b] → R be a real-valued continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on [a,b], which is differentiable
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
on (a,b), differentiable from the right at a, and differentiable from the left at b. Then
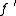 satisfies the intermediate value property: for every t between
satisfies the intermediate value property: for every t between 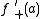 and
and 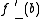 , there is some x in [a,b] such that
, there is some x in [a,b] such that 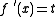 .
.Proof
Without loss of generality we will assume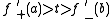 . Let
. Let 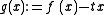 . Then
. Then  exists by hypothesis,
exists by hypothesis, 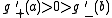 , and we wish to find a zero of
, and we wish to find a zero of  .
.By hypothesis, g is a continuous function on [a,b], by the extreme value theorem
Extreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
it attains a maximum on [a,b]. This maximum cannot be at a, since
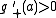 so there should be a point
so there should be a point 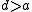 with
with 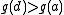 . Similarly,
. Similarly, 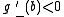 , so g cannot have a maximum at b. So the maximum is attained at some c in (a,b). But then
, so g cannot have a maximum at b. So the maximum is attained at some c in (a,b). But then 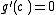 by Fermat's theorem (stationary points)
by Fermat's theorem (stationary points)Fermat's theorem (stationary points)
In mathematics, Fermat's theorem is a method to find local maxima and minima of differentiable functions on open sets by showing that every local extremum of the function is a stationary point...
.
Darboux function
A Darboux function is a real-valued functionReal-valued function
In mathematics, a real-valued function is a function that associates to every element of the domain a real number in the image....
f which has the "intermediate value property": for any two values a and b in the domain of f, and any y between f(a) and f(b), there is some c between a and b with f(c) = y. By the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
, every continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
is a Darboux function. Darboux's contribution was to show that there are discontinuous Darboux functions.
Every discontinuity of a Darboux function is essential, that is, at any point of discontinuity, at least one of the left hand and right hand limits does not exist.
An example of a Darboux function that is discontinuous at one point, is the function
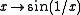 .
.As a consequence of the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
, the derivative of any differentiable function is a Darboux function. In particular, the derivative of the function
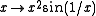 is a Darboux function that is not continuous.
is a Darboux function that is not continuous.An example of a Darboux function that is nowhere continuous is the Conway base 13 function
Conway base 13 function
The Conway base 13 function is a function created by British mathematician John H. Conway as a counterexample to the converse of the intermediate value theorem. In other words, even though Conway's function f is not continuous, if f ...
.
Darboux functions are a quite general class of functions. It turns out that any real-valued function f on the real line can be written as the sum of two Darboux functions. This implies in particular that the class of Darboux functions is not closed under addition.

