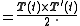Darboux vector
Encyclopedia
In differential geometry, especially the theory of space curves, the Darboux vector is the areal velocity
vector of the Frenet frame
of a space curve. It is named after Gaston Darboux who discovered it. It is also called angular momentum vector, because it is directly proportional to angular momentum
.
In terms of the Frenet-Serret apparatus, the Darboux vector ω can be expressed as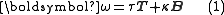
and it has the following symmetrical
properties:
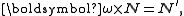
which can be derived from Equation (1) by means of the Frenet-Serret theorem
(or vice versa).
Let a rigid object move along a regular curve described parametrically by β(t). This object has its own intrinsic coordinate system
. As the object moves along the curve, let its intrinsic coordinate system keep itself aligned with the curve's Frenet frame. As it does so, the object's motion will be described by two vectors: a translation vector, and a rotation vector ω, which is an areal velocity vector: the Darboux vector.
Note that this rotation is kinematic
, rather than physical, because usually when a rigid object moves freely in space its rotation is independent of its translation. The exception would be if the object's rotation is physically constrained to align itself with the object's translation, as is the case with the cart of a roller coaster
.
Consider the rigid object moving smoothly along the regular curve. Once the translation is "factored out", the object is seen to rotate the same way as its Frenet frame. The total rotation of the Frenet frame is the combination of the rotations of each of the three Frenet vectors: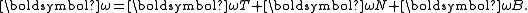
Each Frenet vector moves about an "origin" which is the centre of the rigid object (pick some point within the object and call it its centre). The areal velocity of the tangent vector is: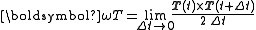
Likewise,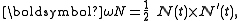
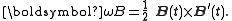
Now apply the Frenet-Serret theorem to find the areal velocity components: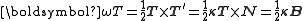
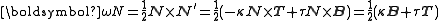
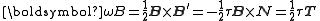
so that
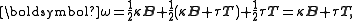
as claimed.
The Darboux vector provides a concise way of interpreting curvature
κ and torsion τ geometrically: curvature is the measure of the rotation of the Frenet frame about the binormal unit vector, whereas torsion is the measure of the rotation of the Frenet frame about the tangent unit vector.
Areal velocity
Areal velocity is the rate at which area is swept out by a particle as it moves along a curve. In many applications, the curve lies in a plane, but in others, it is a space curve....
vector of the Frenet frame
Frenet-Serret formulas
In vector calculus, the Frenet–Serret formulas describe the kinematic properties of a particle which moves along a continuous, differentiable curve in three-dimensional Euclidean space R3...
of a space curve. It is named after Gaston Darboux who discovered it. It is also called angular momentum vector, because it is directly proportional to angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
.
In terms of the Frenet-Serret apparatus, the Darboux vector ω can be expressed as
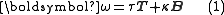
and it has the following symmetrical
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
properties:

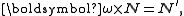
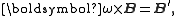
which can be derived from Equation (1) by means of the Frenet-Serret theorem
Frenet-Serret formulas
In vector calculus, the Frenet–Serret formulas describe the kinematic properties of a particle which moves along a continuous, differentiable curve in three-dimensional Euclidean space R3...
(or vice versa).
Let a rigid object move along a regular curve described parametrically by β(t). This object has its own intrinsic coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
. As the object moves along the curve, let its intrinsic coordinate system keep itself aligned with the curve's Frenet frame. As it does so, the object's motion will be described by two vectors: a translation vector, and a rotation vector ω, which is an areal velocity vector: the Darboux vector.
Note that this rotation is kinematic
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
, rather than physical, because usually when a rigid object moves freely in space its rotation is independent of its translation. The exception would be if the object's rotation is physically constrained to align itself with the object's translation, as is the case with the cart of a roller coaster
Roller coaster
The roller coaster is a popular amusement ride developed for amusement parks and modern theme parks. LaMarcus Adna Thompson patented the first coasters on January 20, 1885...
.
Consider the rigid object moving smoothly along the regular curve. Once the translation is "factored out", the object is seen to rotate the same way as its Frenet frame. The total rotation of the Frenet frame is the combination of the rotations of each of the three Frenet vectors:
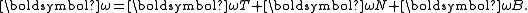
Each Frenet vector moves about an "origin" which is the centre of the rigid object (pick some point within the object and call it its centre). The areal velocity of the tangent vector is:
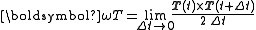
Likewise,
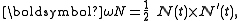
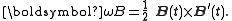
Now apply the Frenet-Serret theorem to find the areal velocity components:
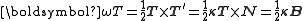
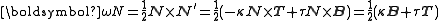
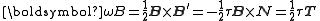
so that
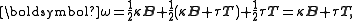
as claimed.
The Darboux vector provides a concise way of interpreting curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
κ and torsion τ geometrically: curvature is the measure of the rotation of the Frenet frame about the binormal unit vector, whereas torsion is the measure of the rotation of the Frenet frame about the tangent unit vector.