
Data Validation and Reconciliation
Encyclopedia
Industrial process data validation and reconciliation or short data validation and reconciliation (DVR) is a technology which is using process information and mathematical methods in order to automatically correct measurements in industrial processes. The use of DVR allows for extracting accurate and reliable information about the state of industry processes from raw measurement data and produces a single consistent set of data representing the most likely process operation.
Models can have different levels of detail, for example one can incorporate simple mass or compound conservation balances, or more advanced thermodynamic models including energy conservation laws. Mathematically the model can be expressed by a nonlinear system of equations in the variables , which incorporates all the above-mentioned system constraints (for example the mass or heat balances around a unit). A variable could be the temperature or the pressure at a certain place in the plant.
can be categorized into two basic types:
Random error
s means that the measurement is a normally distributed random variable
with mean
, where is the true value that is typically not known. A systematic error
on the other hand is characterized by a measurement which is a normally distributed random variable with mean
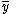 , which is not equal to the true value .
, which is not equal to the true value .
Other sources of error when calculating plant balances, are small instabilities in plant operations. Not all measurements and samples are taken at the same time, causing discrepancies between measurements. Using time averages for plant data partly reduces this problem but lab analyses cannot be averaged.
in production processes where raw measurements were available for all variables
. At the same time the problem of gross error
identification and elimination has been presented . In the late 1960s and 1970s unmeasured variables were taken into account in the data reconciliation process ,. During the 1980s the area of DVR became more mature by considering general nonlinear equation systems coming from thermodynamic models,. In 1992 Liebman et al. introduced the concept of dynamic DVR.
s. From a statistical point of view the main assumption is that no systematic errors exist in the set of measurements, since they may bias the reconciliation results and reduce the robustness of the reconciliation.
Given measurements
measurements 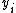 , data reconciliation can mathematically be expressed as an optimization problem
, data reconciliation can mathematically be expressed as an optimization problem
of the following form:
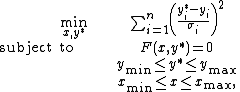
where
is the reconciled value of the -th measurement (), is the measured value of the -th measurement (), is the -th unmeasured variable (), and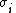 is the standard deviation of the -th measurement (),
is the standard deviation of the -th measurement (),
are the process equality constraints and
are the bounds on the measured and unmeasured variables.
The term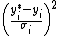 is called the penalty of measurement i. The objective function is the sum of the penalties, which will be denoted in the following by
is called the penalty of measurement i. The objective function is the sum of the penalties, which will be denoted in the following by 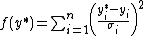 .
.
In other words, one wants to minimize the overall correction (measured in the least squares term) that is needed in order to satisfy the system constraints
. Additionally, each least squares term is weighted by the standard deviation
of the corresponding measurement.
. Redundancy is a source of information that is used to correct the measurements as little as possible in order to satisfy the process constraints. Redundancy can be due to sensor redundancy
, where sensors are duplicated in order to have more than one measurement of the same quantity. Redundancy can also arise from topological redundancy, where a single variable can be estimated in several independent ways, from separate sets of measurements./
Topological redundancy is intimately linked with the degree of freedom
() of a mathematical system , i.e. the minimum number of pieces of information (i.e. measurements) that are required in order to calculate all of the system variables. For instance, in the example above the flow conservation requires that , and it is clear that one needs to know the value of two of the 3 variables in order to calculate the third one. Therefore the degree of freedom in that case is equal to 2.
When speaking about topological redundancy we have to distinguish between measured and unmeasured variables. In the following let us denote by the unmeasured variables and the measured variables. Then the system of the process constraints becomes , which is a nonlinear system in and .
If the system is calculable with the measurements given, then the level of topological redundancy is defined as , i.e. the number of additional measurements that are at hand on top of those measurements which are required in order to just calculate the system. Another way of viewing the level of redundancy is to use the definition of , which is the difference between the number of variables (measured and unmeasured) and the number of equations. Then one gets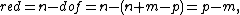
i.e. the redundancy is the difference between the number of equations and the number of unmeasured variables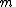 . The level of total redundancy is the sum of sensor redundancy and topological redundancy. We speak of positive redundancy if the system is calculable and the total redundancy is positive. One can see that the level of topological redundancy merely depends on the number of equations (the more equations the higher the redundancy) and the number of unmeasured variables (the more unmeasured variables, the lower the redundancy) and not on the number of measured variables. However, it is possible that the system is not calculable, even though , as illustrated in the following example.
. The level of total redundancy is the sum of sensor redundancy and topological redundancy. We speak of positive redundancy if the system is calculable and the total redundancy is positive. One can see that the level of topological redundancy merely depends on the number of equations (the more equations the higher the redundancy) and the number of unmeasured variables (the more unmeasured variables, the lower the redundancy) and not on the number of measured variables. However, it is possible that the system is not calculable, even though , as illustrated in the following example.
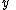 and increase their accuracy and precision: on the one hand they reconciled Further, the data reconciliation problem presented above also includes unmeasured variables
and increase their accuracy and precision: on the one hand they reconciled Further, the data reconciliation problem presented above also includes unmeasured variables 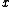 . Based on information redundancy, estimates for these unmeasured variables can be calculated along with their accuracies. In industrial processes these unmeasured variables that data reconciliation provides are referred to as soft sensor
. Based on information redundancy, estimates for these unmeasured variables can be calculated along with their accuracies. In industrial processes these unmeasured variables that data reconciliation provides are referred to as soft sensor
s or virtual sensors, where hardware sensors are not installed.
of several measured values over a well-defined time period.
exist in the set of measured values. These tests can be for example
If no gross errors exist in the set of measured values, then each penalty term in the objective function is a random variable that is normally distributed with mean equal to 0 and variance equal to 1. By consequence, the objective function is a random variable which follows a chi-square distribution, since it is the sum of the square of normally distributed random variables. Comparing the value of the objective function with a given percentile
of the probability density function of a chi-square distribution (e.g. the 95th percentile for a 95% confidence) gives an indication of whether a gross error exists: If , then no gross errors exist with 95% probability. The chi square test gives only a rough indication about the existence of gross errors, and it is easy to conduct: one only has to compare the value of the objective function with the critical value of the chi square distribution.
The individual test compares each penalty term in the objective function with the critical values of the normal distribution. If the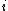 -th penalty term is outside the 95% confidence interval of the normal distribution, then there is reason to believe that this measurement has a gross error.
-th penalty term is outside the 95% confidence interval of the normal distribution, then there is reason to believe that this measurement has a gross error.
to the model, its scope and the level of redundancy
increases. Indeed, as we have seen above, the level of redundancy is defined as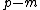 , where
, where 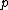 is the number of equations. Including energy balances means adding equations to the system, which results in a higher level of redundancy (provided that enough measurements are available, or equivalently, not too many variables are unmeasured).
is the number of equations. Including energy balances means adding equations to the system, which results in a higher level of redundancy (provided that enough measurements are available, or equivalently, not too many variables are unmeasured).
the reconciliation results. Therefore it is important to identify and eliminate these gross errors from the reconciliation process. After the reconciliation statistical tests can be applied that indicate whether or not a gross error does exist somewhere in the set of measurements. These techniques of gross error remediation are based on two concepts:
Gross error elimination determines one measurement that is biased by a systematic error and discards this measurement from the data set. The determination of the measurement to be discarded is based on different kinds of penalty terms that express how much the measured values deviate from the reconciled values. Once the gross errors are detected they are discarded from the measurements and the reconciliation can be done without these faulty measurements that spoil the reconciliation process. If needed, the elimination is repeated until no gross error exists in the set of measurements.
Gross error relaxation targets at relaxing the estimate for the uncertainty of suspicious measurements so that the reconciled value is in the 95% confidence interval. Relaxation typically finds application when it is not possible to determine which measurement around one unit is responsible for the gross error (equivalence of gross errors). Then measurement uncertainties of the measurements involved are increased.
It is important to note that the remediation of gross errors reduces the quality of the reconciliation, either the redundancy decreases (elimination) or the uncertainty of the measured. Therefore it can only be applied when the initial level of redundancy is high enough to ensure that the data reconciliation can still be done (see Section 2,).
The result of an advanced DVR procedure is a coherent set of validated and reconciled process data.
are difficult or expensive to position (see ); or where accurate data is of high importance, for example for security reasons in nuclear power plants (see ). Another field of application is performance and process monitoring
(see ) in oil refining or in the chemical industry.
As DVR enables to calculate estimates even for unmeasured variables in a reliable way, the German Engineering Society (VDI Gesellschaft Energie und Umwelt) has accepted the technology of DVR as a means to replace expensive sensors in the nuclear power industry (see VDI norm 2048,).
White papers:
Models, data and measurement errors
Industrial processes, for example chemical or thermodynamic processes in chemical plants, refineries, oil or gas production sites, or power plants, are often represented by two fundamental means:- Models that express the general structure of the processes,
- Data that reflects the state of the processes at a given point in time.
Models can have different levels of detail, for example one can incorporate simple mass or compound conservation balances, or more advanced thermodynamic models including energy conservation laws. Mathematically the model can be expressed by a nonlinear system of equations in the variables , which incorporates all the above-mentioned system constraints (for example the mass or heat balances around a unit). A variable could be the temperature or the pressure at a certain place in the plant.
Error types
Data originates typically from measurements taken at different places throughout the industrial site, for example temperature, pressure, volumetric flow rate measurements etc. To understand the basic principles of DVR, it is important to first recognize that plant measurements are never 100% correct, i.e. raw measurement is not a solution of the nonlinear system . When using measurements without correction to generate plant balances, it is common to have incoherencies. Measurement errorsObservational error
Observational error is the difference between a measured value of quantity and its true value. In statistics, an error is not a "mistake". Variability is an inherent part of things being measured and of the measurement process.-Science and experiments:...
can be categorized into two basic types:
- random errorRandom errorRandom errors are errors in measurement that lead to measurable values being inconsistent when repeated measures of a constant attribute or quantity are taken...
s due to intrinsic sensorSensorA sensor is a device that measures a physical quantity and converts it into a signal which can be read by an observer or by an instrument. For example, a mercury-in-glass thermometer converts the measured temperature into expansion and contraction of a liquid which can be read on a calibrated...
accuracy and - systematic errors (or gross errors) due to sensor calibrationCalibrationCalibration is a comparison between measurements – one of known magnitude or correctness made or set with one device and another measurement made in as similar a way as possible with a second device....
or faulty data transmission.
Random error
Random error
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measures of a constant attribute or quantity are taken...
s means that the measurement is a normally distributed random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
, where is the true value that is typically not known. A systematic error
Systematic error
Systematic errors are biases in measurement which lead to the situation where the mean of many separate measurements differs significantly from the actual value of the measured attribute. All measurements are prone to systematic errors, often of several different types...
on the other hand is characterized by a measurement which is a normally distributed random variable with mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
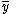 , which is not equal to the true value .
, which is not equal to the true value .Other sources of error when calculating plant balances, are small instabilities in plant operations. Not all measurements and samples are taken at the same time, causing discrepancies between measurements. Using time averages for plant data partly reduces this problem but lab analyses cannot be averaged.
Necessity of removing measurement errors
ISA-95 is the international standard for the integration of enterprise and control systems . It asserts that:Data reconciliation is a serious issue for enterprise-control integration. The data have to be valid to be useful for the enterprise system. The data must often be determined from physical measurements that have associated error factors. This must usually be converted into exact values for the enterprise system. This conversion may require manual, or intelligent reconciliation of the converted values [...].
Systems must be set up to ensure that accurate data are sent to production and from production. Inadvertent operator or clerical errors may result in too much production, too little production, the wrong production, incorrect inventory, or missing inventory.
History
DVR has become more and more important due to industrial processes that are becoming more and more complex. DVR started in the early 1960s with applications aiming at closing material balancesMass balance
A mass balance is an application of conservation of mass to the analysis of physical systems. By accounting for material entering and leaving a system, mass flows can be identified which might have been unknown, or difficult to measure without this technique...
in production processes where raw measurements were available for all variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
. At the same time the problem of gross error
Systematic error
Systematic errors are biases in measurement which lead to the situation where the mean of many separate measurements differs significantly from the actual value of the measured attribute. All measurements are prone to systematic errors, often of several different types...
identification and elimination has been presented . In the late 1960s and 1970s unmeasured variables were taken into account in the data reconciliation process ,. During the 1980s the area of DVR became more mature by considering general nonlinear equation systems coming from thermodynamic models,. In 1992 Liebman et al. introduced the concept of dynamic DVR.
Data reconciliation
Data reconciliation is a technique that targets at correcting measurement errors that are due to measurement noise, i.e. random errorRandom error
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measures of a constant attribute or quantity are taken...
s. From a statistical point of view the main assumption is that no systematic errors exist in the set of measurements, since they may bias the reconciliation results and reduce the robustness of the reconciliation.
Given
 measurements
measurements 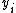 , data reconciliation can mathematically be expressed as an optimization problem
, data reconciliation can mathematically be expressed as an optimization problemOptimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
of the following form:
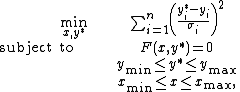
where
is the reconciled value of the -th measurement (), is the measured value of the -th measurement (), is the -th unmeasured variable (), and
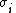 is the standard deviation of the -th measurement (),
is the standard deviation of the -th measurement (),are the process equality constraints and
are the bounds on the measured and unmeasured variables.
The term
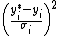 is called the penalty of measurement i. The objective function is the sum of the penalties, which will be denoted in the following by
is called the penalty of measurement i. The objective function is the sum of the penalties, which will be denoted in the following by 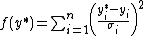 .
.In other words, one wants to minimize the overall correction (measured in the least squares term) that is needed in order to satisfy the system constraints
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
. Additionally, each least squares term is weighted by the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of the corresponding measurement.
Redundancy
Data reconciliation is strongly relying on the concept of redundancyRedundancy (information theory)
Redundancy in information theory is the number of bits used to transmit a message minus the number of bits of actual information in the message. Informally, it is the amount of wasted "space" used to transmit certain data...
. Redundancy is a source of information that is used to correct the measurements as little as possible in order to satisfy the process constraints. Redundancy can be due to sensor redundancy
Redundancy (engineering)
In engineering, redundancy is the duplication of critical components or functions of a system with the intention of increasing reliability of the system, usually in the case of a backup or fail-safe....
, where sensors are duplicated in order to have more than one measurement of the same quantity. Redundancy can also arise from topological redundancy, where a single variable can be estimated in several independent ways, from separate sets of measurements./
Topological redundancy is intimately linked with the degree of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
() of a mathematical system , i.e. the minimum number of pieces of information (i.e. measurements) that are required in order to calculate all of the system variables. For instance, in the example above the flow conservation requires that , and it is clear that one needs to know the value of two of the 3 variables in order to calculate the third one. Therefore the degree of freedom in that case is equal to 2.
When speaking about topological redundancy we have to distinguish between measured and unmeasured variables. In the following let us denote by the unmeasured variables and the measured variables. Then the system of the process constraints becomes , which is a nonlinear system in and .
If the system is calculable with the measurements given, then the level of topological redundancy is defined as , i.e. the number of additional measurements that are at hand on top of those measurements which are required in order to just calculate the system. Another way of viewing the level of redundancy is to use the definition of , which is the difference between the number of variables (measured and unmeasured) and the number of equations. Then one gets
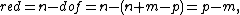
i.e. the redundancy is the difference between the number of equations and the number of unmeasured variables
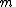 . The level of total redundancy is the sum of sensor redundancy and topological redundancy. We speak of positive redundancy if the system is calculable and the total redundancy is positive. One can see that the level of topological redundancy merely depends on the number of equations (the more equations the higher the redundancy) and the number of unmeasured variables (the more unmeasured variables, the lower the redundancy) and not on the number of measured variables. However, it is possible that the system is not calculable, even though , as illustrated in the following example.
. The level of total redundancy is the sum of sensor redundancy and topological redundancy. We speak of positive redundancy if the system is calculable and the total redundancy is positive. One can see that the level of topological redundancy merely depends on the number of equations (the more equations the higher the redundancy) and the number of unmeasured variables (the more unmeasured variables, the lower the redundancy) and not on the number of measured variables. However, it is possible that the system is not calculable, even though , as illustrated in the following example.Example of calculable and non-calculable systems
Let us consider a small system with 4 streams and 2 units. We incorporate only flow conservation constraints and obtain and . If we have measurements for and , but not for and , then the system cannot be calculated (knowing does not give information about and ). On the other hand, if and are known, but not and , then the system can be calculated.Benefits
Redundancy can be used as a source of information to cross-check and correct the measurements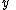 and increase their accuracy and precision: on the one hand they reconciled Further, the data reconciliation problem presented above also includes unmeasured variables
and increase their accuracy and precision: on the one hand they reconciled Further, the data reconciliation problem presented above also includes unmeasured variables 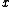 . Based on information redundancy, estimates for these unmeasured variables can be calculated along with their accuracies. In industrial processes these unmeasured variables that data reconciliation provides are referred to as soft sensor
. Based on information redundancy, estimates for these unmeasured variables can be calculated along with their accuracies. In industrial processes these unmeasured variables that data reconciliation provides are referred to as soft sensorSoft sensor
Soft sensor or virtual sensor is a common name for software where several measurements are processed together. There may be dozens or even hundreds of measurements. The interaction of the signals can be used for calculating new quantities that need not be measured...
s or virtual sensors, where hardware sensors are not installed.
Data Validation
Data validation denotes all validation and verification actions before and after the reconciliation step.Data Filtering
Data filtering denotes the process of treating measured data such that the values become meaningful and lie within the range of expected values. Data filtering is necessary before the reconciliation process in order to increase robustness of the reconciliation step. There are several ways of data filtering, for example taking the averageAverage
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
of several measured values over a well-defined time period.
Result Validation
Result validation is the set of validation or verification actions taken after the reconciliation process and it takes into account measured and unmeasured variables as well as reconciled values. Result validation covers, but is not limited to, penalty analysis for determining the reliability of the reconciliation, or bound checks to ensure that the reconciled values lie in a certain range, e.g. the temperature has to be within some reasonable bounds.Gross Error Detection
Result validation may include statistical tests to validate the reliability of the reconciled values, by checking whether gross errorsSystematic error
Systematic errors are biases in measurement which lead to the situation where the mean of many separate measurements differs significantly from the actual value of the measured attribute. All measurements are prone to systematic errors, often of several different types...
exist in the set of measured values. These tests can be for example
- the chi square test (global test)
- the individual test.
If no gross errors exist in the set of measured values, then each penalty term in the objective function is a random variable that is normally distributed with mean equal to 0 and variance equal to 1. By consequence, the objective function is a random variable which follows a chi-square distribution, since it is the sum of the square of normally distributed random variables. Comparing the value of the objective function with a given percentile
Percentile
In statistics, a percentile is the value of a variable below which a certain percent of observations fall. For example, the 20th percentile is the value below which 20 percent of the observations may be found...
of the probability density function of a chi-square distribution (e.g. the 95th percentile for a 95% confidence) gives an indication of whether a gross error exists: If , then no gross errors exist with 95% probability. The chi square test gives only a rough indication about the existence of gross errors, and it is easy to conduct: one only has to compare the value of the objective function with the critical value of the chi square distribution.
The individual test compares each penalty term in the objective function with the critical values of the normal distribution. If the
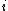 -th penalty term is outside the 95% confidence interval of the normal distribution, then there is reason to believe that this measurement has a gross error.
-th penalty term is outside the 95% confidence interval of the normal distribution, then there is reason to believe that this measurement has a gross error.Advanced Data Validation and Reconciliation
Advanced data validation and reconciliation (DVR) is an integrated approach of combining data reconciliation and data validation techniques, which is characterized by- complex models incorporating besides mass balances also thermodynamics, momentum balances, equilibria constraints, hydrodynamics etc.
- gross error remediation techniques to ensure meaningfulness of the reconciled values,
- robust algorithms for solving the reconciliation problem.
Thermodynamic models
Simple models include mass balances only. When adding thermodynamic constraints such as heat balancesEnergy balance
Energy balance may refer to:* First law of thermodynamics, according to which energy cannot be created or destroyed, only modified in form* Energy balance , a measurement of the biological homeostasis of energy in living systems...
to the model, its scope and the level of redundancy
Data redundancy
Data redundancy occurs in database systems which have a field that is repeated in two or more tables. For instance, in case when customer data is duplicated and attached with each product bought then redundancy of data is a known source of inconsistency, since customer might appear with different...
increases. Indeed, as we have seen above, the level of redundancy is defined as
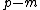 , where
, where 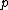 is the number of equations. Including energy balances means adding equations to the system, which results in a higher level of redundancy (provided that enough measurements are available, or equivalently, not too many variables are unmeasured).
is the number of equations. Including energy balances means adding equations to the system, which results in a higher level of redundancy (provided that enough measurements are available, or equivalently, not too many variables are unmeasured).Gross Error Remediation
Gross errors are measurement systematic errors that may biasBias
Bias is an inclination to present or hold a partial perspective at the expense of alternatives. Bias can come in many forms.-In judgement and decision making:...
the reconciliation results. Therefore it is important to identify and eliminate these gross errors from the reconciliation process. After the reconciliation statistical tests can be applied that indicate whether or not a gross error does exist somewhere in the set of measurements. These techniques of gross error remediation are based on two concepts:
- gross error elimination
- gross error relaxation.
Gross error elimination determines one measurement that is biased by a systematic error and discards this measurement from the data set. The determination of the measurement to be discarded is based on different kinds of penalty terms that express how much the measured values deviate from the reconciled values. Once the gross errors are detected they are discarded from the measurements and the reconciliation can be done without these faulty measurements that spoil the reconciliation process. If needed, the elimination is repeated until no gross error exists in the set of measurements.
Gross error relaxation targets at relaxing the estimate for the uncertainty of suspicious measurements so that the reconciled value is in the 95% confidence interval. Relaxation typically finds application when it is not possible to determine which measurement around one unit is responsible for the gross error (equivalence of gross errors). Then measurement uncertainties of the measurements involved are increased.
It is important to note that the remediation of gross errors reduces the quality of the reconciliation, either the redundancy decreases (elimination) or the uncertainty of the measured. Therefore it can only be applied when the initial level of redundancy is high enough to ensure that the data reconciliation can still be done (see Section 2,).
Workflow
Advanced DVR solutions offer an integration of the techniques mentioned above:- data acquisition from data historian, data base or manual inputs
- data validation and filtering of raw measurements
- data reconciliation of filtered measurements
- result verification
- range check
- gross error remediation (and go back to step 3)
- result storage (raw measurements together with reconciled values)
The result of an advanced DVR procedure is a coherent set of validated and reconciled process data.
Applications
DVR finds application mainly in industry sectors where either measurements are not accurate or even non-existing, like for example in the upstream sector where flow metersFlow measurement
Flow measurement is the quantification of bulk fluid movement. Flow can be measured in a variety of ways.Positive-displacement flow meters acumulate a fixed volume of fluid and then count the number of times the volume is filled to measure flow...
are difficult or expensive to position (see ); or where accurate data is of high importance, for example for security reasons in nuclear power plants (see ). Another field of application is performance and process monitoring
Performance testing
In software engineering, performance testing is in general testing performed to determine how a system performs in terms of responsiveness and stability under a particular workload...
(see ) in oil refining or in the chemical industry.
As DVR enables to calculate estimates even for unmeasured variables in a reliable way, the German Engineering Society (VDI Gesellschaft Energie und Umwelt) has accepted the technology of DVR as a means to replace expensive sensors in the nuclear power industry (see VDI norm 2048,).
See also
- Process simulationProcess simulationProcess simulation is used for the design, development, analysis, and optimization of technical processes and is mainly applied to chemical plants and chemical processes, but also to power stations, and similar technical facilities.- Main principle :...
- Pinch analysisPinch analysisPinch analysis is a methodology for minimising energy consumption of chemical processes by calculating thermodynamically feasible energy targets and achieving them by optimising heat recovery systems, energy supply methods and process operating conditions...
- Industrial processes
- Chemical EngineeringChemical engineeringChemical engineering is the branch of engineering that deals with physical science , and life sciences with mathematics and economics, to the process of converting raw materials or chemicals into more useful or valuable forms...
DVR Software
- ROMeo ( ROMeo Online Performance Suite)
- Sigmafine (Visiant Pimsoft)
- CADSIM Plus(CADSIM Plus)
- S-TMS (Soteica)
External links
Some research groups working on data reconciliation:- Process and product design - Plant operations, University of Oklahoma, USA
- Indian Institute of Technology Madras, India
- Laboratory for Analysis and Synthesis of Chemical Systems, University of Liege, Belgium
- Industrial Energy Systems Laboratory, Lausanne, Switzerland
White papers:

