Davenport–Schinzel sequence
Encyclopedia
In combinatorics
, a Davenport–Schinzel sequence is a sequence
of symbols in which the number of times any two symbols may appear in alternation is limited. The maximum possible length of a Davenport–Schinzel sequence is bounded by the number of its distinct symbols multiplied by a small but nonconstant factor that depends on the number of alternations that are allowed. Davenport–Schinzel sequences were first defined in 1965 by Harold Davenport
and Andrzej Schinzel
to analyze linear differential equation
s. Following these sequences and their length bounds have also become a standard tool in discrete geometry
and in the analysis of geometric algorithms
.
For instance, the sequence
is a Davenport–Schinzel sequence of order 3: it contains alternating subsequences of length four, such as ...1, ... 2, ... 1, ... 2, ... (which appears in four different ways as a subsequence of the whole sequence) but it does not contain any alternating subsequences of length five.
If a Davenport–Schinzel sequence of order s includes n distinct values, it is called an (n,s) Davenport–Schinzel sequence, or a DS(n,s)-sequence.
where A is the Ackermann function. Due to the very rapid growth of the Ackermann function, its inverse α grows very slowly, and is at most four for problems of any practical size.
Using big O and big Θ notation
, the following bounds are known:
However, this bound is not known to be tight.
The value of λs(n) is also known when s is variable but n is a small constant:


 The lower envelope of a set of functions ƒi(x) of a real variable x is the function given by their pointwise minimum:
The lower envelope of a set of functions ƒi(x) of a real variable x is the function given by their pointwise minimum:
Suppose that these functions are particularly well behaved: they are all continuous
, and any two of them are equal on at most s values. With these assumptions, the real line can be partitioned into finitely many interval
s within which one function has values smaller than all of the other functions. The sequence of these intervals, labeled by the minimizing function within each interval, forms a Davenport–Schinzel sequence of order s. Thus, any upper bound on the complexity of a Davenport–Schinzel sequence of this order also bounds the number of intervals in this representation of the lower envelope.
In the original application of Davenport and Schinzel, the functions under consideration were a set of different solutions to the same homogeneous linear differential equation
of order s. Any two distinct solutions can have at most s values in common, so the lower envelope of a set of n distinct solutions forms a DS(n,s)-sequence.
The same concept of a lower envelope can also be applied to functions that are only piecewise
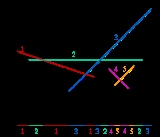
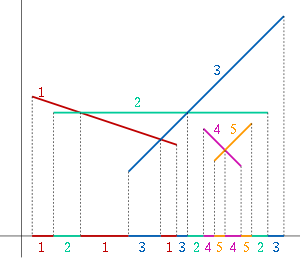
continuous or that are defined only over intervals of the real line; however, in this case, the points of discontinuity of the functions and the endpoints of the interval within which each function is defined add to the order of the sequence. For instance, a non-vertical line segment in the plane can be interpreted as the graph of a function
mapping an interval of x values to their corresponding y values, and the lower envelope of a collection of line segments forms a Davenport–Schinzel sequence of order three because any two line segments can form an alternating subsequence with length at most four.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, a Davenport–Schinzel sequence is a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of symbols in which the number of times any two symbols may appear in alternation is limited. The maximum possible length of a Davenport–Schinzel sequence is bounded by the number of its distinct symbols multiplied by a small but nonconstant factor that depends on the number of alternations that are allowed. Davenport–Schinzel sequences were first defined in 1965 by Harold Davenport
Harold Davenport
Harold Davenport FRS was an English mathematician, known for his extensive work in number theory.-Early life:...
and Andrzej Schinzel
Andrzej Schinzel
Andrzej Bobola Maria Schinzel is a Polish mathematician, studying mainly number theory.- Biography :Schinzel received his Ph.D...
to analyze linear differential equation
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
s. Following these sequences and their length bounds have also become a standard tool in discrete geometry
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
and in the analysis of geometric algorithms
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
.
Definition
A finite sequence U = u1, u2, u3, is said to be a Davenport–Schinzel sequence of order s if it satisfies the following two properties:- No two consecutive values in the sequence are equal to each other.
- If x and y are two distinct values occurring in the sequence, then the sequence does not contain a subsequence ... x, ... y, ..., x, ..., y, ... consisting of s + 2 values alternating between x and y.
For instance, the sequence
- 1, 2, 1, 3, 1, 3, 2, 4, 5, 4, 5, 2, 3
is a Davenport–Schinzel sequence of order 3: it contains alternating subsequences of length four, such as ...1, ... 2, ... 1, ... 2, ... (which appears in four different ways as a subsequence of the whole sequence) but it does not contain any alternating subsequences of length five.
If a Davenport–Schinzel sequence of order s includes n distinct values, it is called an (n,s) Davenport–Schinzel sequence, or a DS(n,s)-sequence.
Length bounds
The complexity of DS(n,s)-sequence has been analyzed asymptotically in the limit as n goes to infinity, with the assumption that s is a fixed constant, and nearly tight bounds are known for all s. Let λs(n) denote the length of the longest DS(n,s)-sequence. The best bounds known on λs involve the inverse Ackermann function- α(n) = min { m | A(m,m) ≥ n },
where A is the Ackermann function. Due to the very rapid growth of the Ackermann function, its inverse α grows very slowly, and is at most four for problems of any practical size.
Using big O and big Θ notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
, the following bounds are known:
- λ1(n) = n.
- λ2(n) = 2n − 1.
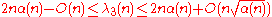 . This complexity bound can be realized to within a constant factor by line segments: there exist arrangements of n line segments in the plane whose lower envelopes have complexity Ω(n α(n)).
. This complexity bound can be realized to within a constant factor by line segments: there exist arrangements of n line segments in the plane whose lower envelopes have complexity Ω(n α(n)).- For even values of s ≥ 4,
-
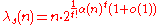 , where t = (s − 2)/2.
, where t = (s − 2)/2.
- For odd values of s ≥ 5 the best known upper bound is
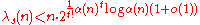 , where t = (s − 3)/2.
, where t = (s − 3)/2.
However, this bound is not known to be tight.
The value of λs(n) is also known when s is variable but n is a small constant:



Application to lower envelopes

- ƒ(x) = miniƒi(x).
Suppose that these functions are particularly well behaved: they are all continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, and any two of them are equal on at most s values. With these assumptions, the real line can be partitioned into finitely many interval
Interval
Interval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...
s within which one function has values smaller than all of the other functions. The sequence of these intervals, labeled by the minimizing function within each interval, forms a Davenport–Schinzel sequence of order s. Thus, any upper bound on the complexity of a Davenport–Schinzel sequence of this order also bounds the number of intervals in this representation of the lower envelope.
In the original application of Davenport and Schinzel, the functions under consideration were a set of different solutions to the same homogeneous linear differential equation
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
of order s. Any two distinct solutions can have at most s values in common, so the lower envelope of a set of n distinct solutions forms a DS(n,s)-sequence.
The same concept of a lower envelope can also be applied to functions that are only piecewise
Piecewise
On mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
continuous or that are defined only over intervals of the real line; however, in this case, the points of discontinuity of the functions and the endpoints of the interval within which each function is defined add to the order of the sequence. For instance, a non-vertical line segment in the plane can be interpreted as the graph of a function
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
mapping an interval of x values to their corresponding y values, and the lower envelope of a collection of line segments forms a Davenport–Schinzel sequence of order three because any two line segments can form an alternating subsequence with length at most four.
External links
- Davenport-Schinzel Sequence, from MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
. - Davenport-Schinzel Sequences, a section in the book Motion Planning, by Steven M. LaValle.

