Debye-Waller factor
Encyclopedia
The Debye–Waller factor named after Peter Debye
and Ivar Waller
, is used in condensed matter physics
to describe the attenuation of x-ray scattering or coherent neutron scattering
caused by thermal motion. It has also been called the B factor or the temperature factor. Often, "Debye-Waller factor" is used as a generic term that comprises the Lamb-Mössbauer factor of incoherent neutron scattering and Mössbauer spectroscopy.
The DWF depends on the scattering vector q. For a given q, DWF(q) gives the fraction of elastic scattering; 1-DWF(q) correspondingly gives the fraction of inelastic scattering. In diffraction
studies, only the elastic scattering is useful; in crystals, it gives rise to distinct Bragg peak
s. Inelastic scattering events are undesirable as they cause a diffuse background — unless the energies of scattered particles are analysed, in which case they carry valuable information (inelastic neutron scattering
).
The basic expression for the DWF is given by
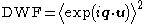
where u is the displacement of a scattering center,
and <...> denotes either thermal or time averaging.
Assuming harmonicity
of the scattering centers in the material under study, the Boltzmann distribution
implies that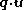
is normally distributed with zero mean. Then, using for example the expression of the corresponding characteristic function
, the DWF takes the form
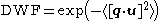
Note that although the above reasoning is classical, the same holds also quantum mechanically.
Assuming also isotropy
of the harmonic potential, one may write
where q, u are the magnitudes (or absolute values) of the vectors q, u respectively.
Note that if the incident wave has wavelength λ, and it is elastically scattered by an angle of 2θ, then q = 4π sin(θ) / λ.
In the context of protein structure
s, the B-factors can be taken as indicating the relative vibrational motion of different parts of the structure. Atoms with low B-factors belong to a part of the structure that is well-ordered. Atoms with large B-factors generally belong to part of the structure that is very flexible. Each ATOM record (PDB file format
) of a crystal structure deposited with the Protein Data Bank
contains a B-factor for that atom.
Peter Debye
Peter Joseph William Debye FRS was a Dutch physicist and physical chemist, and Nobel laureate in Chemistry.-Early life:...
and Ivar Waller
Ivar Waller
Ivar Waller was a Swedish professor of theoretical physics at Uppsala University. He developed the theory of X-ray scattering by lattice vibrations of a crystal, building upon the prior work of Peter Debye...
, is used in condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
to describe the attenuation of x-ray scattering or coherent neutron scattering
Neutron scattering
Neutron scattering,the scattering of free neutrons by matter,is a physical processand an experimental technique using this processfor the investigation of materials.Neutron scattering as a physical process is of primordial importance...
caused by thermal motion. It has also been called the B factor or the temperature factor. Often, "Debye-Waller factor" is used as a generic term that comprises the Lamb-Mössbauer factor of incoherent neutron scattering and Mössbauer spectroscopy.
The DWF depends on the scattering vector q. For a given q, DWF(q) gives the fraction of elastic scattering; 1-DWF(q) correspondingly gives the fraction of inelastic scattering. In diffraction
Diffraction
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
studies, only the elastic scattering is useful; in crystals, it gives rise to distinct Bragg peak
Bragg Peak
The Bragg peak is a pronounced peak on the Bragg curve which plots the energy loss of ionizing radiation during its travel through matter. For protons, α-rays, and other ion rays, the peak occurs immediately before the particles come to rest...
s. Inelastic scattering events are undesirable as they cause a diffuse background — unless the energies of scattered particles are analysed, in which case they carry valuable information (inelastic neutron scattering
Inelastic neutron scattering
Inelastic neutron scattering is an experimental technique commonly used in condensed matter research to study atomic and molecular motion as well as magnetic and crystal field excitations....
).
The basic expression for the DWF is given by
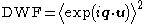
where u is the displacement of a scattering center,
and <...> denotes either thermal or time averaging.
Assuming harmonicity
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
of the scattering centers in the material under study, the Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
implies that
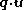is normally distributed with zero mean. Then, using for example the expression of the corresponding characteristic functionCharacteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
, the DWF takes the form
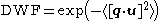
Note that although the above reasoning is classical, the same holds also quantum mechanically.
Assuming also isotropy
Isotropy
Isotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary...
of the harmonic potential, one may write
where q, u are the magnitudes (or absolute values) of the vectors q, u respectively.
Note that if the incident wave has wavelength λ, and it is elastically scattered by an angle of 2θ, then q = 4π sin(θ) / λ.
In the context of protein structure
Protein structure
Proteins are an important class of biological macromolecules present in all organisms. Proteins are polymers of amino acids. Classified by their physical size, proteins are nanoparticles . Each protein polymer – also known as a polypeptide – consists of a sequence formed from 20 possible L-α-amino...
s, the B-factors can be taken as indicating the relative vibrational motion of different parts of the structure. Atoms with low B-factors belong to a part of the structure that is well-ordered. Atoms with large B-factors generally belong to part of the structure that is very flexible. Each ATOM record (PDB file format
Protein Data Bank (file format)
The Protein Data Bank file format is a textual file format describing the three dimensional structures of molecules held in the Protein Data Bank. The pdb format accordingly provides for description and annotation of protein and nucleic acid structures including atomic coordinates, observed...
) of a crystal structure deposited with the Protein Data Bank
Protein Data Bank
The Protein Data Bank is a repository for the 3-D structural data of large biological molecules, such as proteins and nucleic acids....
contains a B-factor for that atom.