Decoherence-free subspaces
Encyclopedia
A decoherence-free subspace (DFS) is a subspace
of a system's Hilbert space
that is invariant
to non-unitary
dynamics. Alternatively stated, they are a small section of the system Hilbert space where the system is decoupled
from the environment and thus its evolution is completely unitary. DFSs can also be characterized as a special class of quantum error correcting codes. In this representation they are passive error-preventing codes since these subspaces are encoded with information that (possibly) won't require any active stabilization methods. These subspaces prevent destructive environmental interactions by isolating quantum information
. As such, they are an important subject in quantum computing, where (coherent
) control of quantum systems is the desired goal. Decoherence
creates problems in this regard by causing loss of coherence between the quantum states of a system and therefore the decay of their interference
terms, thus leading to loss of information from the (open) quantum system to the surrounding environment. Since quantum computers cannot be isolated from their environment (i.e. we cannot have a truly isolated quantum system in the real world) and information can be lost, the study of DFSs is important for the implementation of quantum computers into the real world.
, who studied the consequences of pure dephasing on two qubits that have the same interaction with the environment. They found that two such qubits do not decohere. Originally the term "sub-decoherence" was used by Palma to describe this situation.
s. Their analysis gave the first formal and general circumstances for the existence of decoherence-free (DF) states, which did not rely upon knowing the system-environment coupling strength. Zanardi and Rasetti called these DF states "error avoiding codes". Subsequently, Daniel A. Lidar
proposed the title "decoherence-free subspace" for the space in which these DF states exist. Lidar studied the strength of DF states against perturbation
s and discovered that the coherence prevalent in DF states can be upset by evolution of the system Hamiltonian. This observation discerned another prerequisite for the possible use of DF states for quantum computation. A thoroughly general requirement for the existence of DF states was obtained by Lidar, D. Bacon, and K.B. Whaley expressed in terms of the Kraus operator-sum representation (OSR).
, and L. Viola introduced the concept of a "noiseless subsystem". Knill extended to higher-dimensional irreducible representations of the algebra
generating the dynamical symmetry in the system-environment interaction. Earlier work on DFSs described DF states as singlets, which are one-dimensional irreducible representations. This work proved to be successful, as a result of this analysis was the lowering of the number of qubits required to build a DFS under collective decoherence from four to three. The generalization from subspaces to subsystems formed a foundation for combining most known decoherence prevention and nulling strategies.
,
where the interaction Hamiltonian
is given in the usual way as
and where
act upon the system(bath) only, and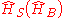 
is the system(bath) Hamiltonian, and 
is the identity operator acting on the system (bath).
Under these conditions, the dynamical evolution within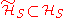
, where 
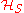is the system Hilbert space, is completely unitary 
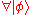(all possible bath states) if and only if:
(i)
that span
and 
, the space of bounded system-bath operators on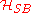 
,
(ii) the system and bath are not coupled at first (i.e. they can be represented as a product state),
(iii) there is no "leakage" of states out of
; that is, the system Hamiltonian 
does not map the states 
out of 
.
In other words, if the system begins in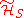
(i.e. the system and bath are initially decoupled) and the system Hamiltonian 
leaves 
invariant, then 
is a DFS if and only if it satisfies (i).
These states are degenerate
eigenkets of
and thus are distinguishable, hence preserving information in certain decohering processes. Any subspace of the system Hilbert space that satisfies the above conditions is a decoherence-free subspace. However, information can still "leak" out of this subspace if condition (iii) is not satisfied. Therefore, even if a DFS exists under the Hamiltonian conditions, there are still non-unitary actions that can act upon these subspaces and take states out of them into another subspace, which may or may not be a DFS, of the system Hilbert space.
be an N-dimensional DFS, where 
is the system's (the quantum system alone) Hilbert space. The Kraus operators when written in terms of the N basis states that span
are given as:
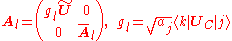
where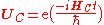
(
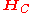is the combined system-bath Hamiltonian), 
acts on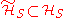 
, and 
is an arbitrary matrix that acts on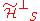 
(the orthogonal complement to 
). Since 
operates on 
, then it will not create decoherence in 
; however, it can (possibly) create decohering effects in 
. Consider the basis kets 
which span 
and, furthermore, they fulfill:
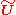is an arbitrary unitary operator
and may or may not be time-dependent, but it is independent of the indexing variable
. The 
's are complex
constants. Since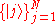
spans 
, then any pure state 
can be written as a linear combination
of these basis kets:
This state will be decoherence-free; this can be seen by considering the action of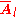
on 
:
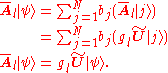
Therefore, in terms of the density operator representation of
, 
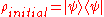, the evolution of this state is:
The above expression says that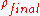
is a pure state and that its evolution is unitary, since 
is unitary. Therefore, any state in 
will not decohere since its evolution is governed by a unitary operator and so its dynamical evolution will be completely unitary. Thus 
is a decoherence-free subspace.
The above argument can be generalized to an initial arbitrary mixed state as well.
, where 
is the density operator representation of the state of the system, the dynamics will be decoherence-free.
Let
span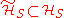 
, where 
is the system's Hilbert space. Under the assumptions that:
a necessary and sufficient condition of for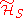
to be a DFS is 
:
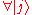The above expression states that all basis states
are degenerate eigenstates of the error generators 
As such, their respective coherence terms do not decohere. Thus states within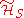 
will remain mutually distinguishable after a decohering process since their respective eigenvalues are degenerate and hence identifiable after action under the error generators.
-a non-negative (i.e. its eigenvalues are positive), trace-preserving 
, 
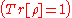density operator that belongs to the system's Hilbert-Schmidt space, the space of bounded operator
s on
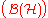. Suppose that this density operator(state) is selected from a set of states 
, a DFS of 
(the system's Hilbert space) and where 
.
This set of states is called a code, because the states within this set encode particular kind of information; that is, the set S encodes information through its states. This information that is contained within
must be able to be accessed; since the information is encoded in the states in 
, these states must be distinguishable to some process, 
say, that attempts to acquire the information. Therefore, for two states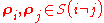 
, the process 
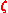is information preserving for these states if the states 
remain as distinguishable after the process as they were before it. Stated in a more general manner, a code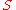 
(or DFS) is preserved by a process 
iff each pair of states 
is as distinguishable after 
is applied as they were before it was applied. A more practical description would be: 
is preserved by a process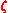 
if and only if 
and 
This just says that
is a 1:1 trace-distance-preserving map on 
. In this picture DFSs are sets of states (codes rather) whose mutual distinguishability is unaffected by a process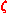 
.
Consider a code
, which is a subspace of the system Hilbert space, with encoded information given by 
(i.e. the "codewords"). This code can be implemented to protect against decoherence and thus prevent loss of information in a small section of the system's Hilbert space. The errors are caused by interaction of the system with the environment (bath) and are represented by the Kraus operators. After the system has interacted with the bath, the information contained within 
must be able to be "decoded"; therefore, to retrieve this information a recovery operator 
is introduced. So a QECC is a subspace 
along with a set of recovery operators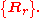 
Let
be a QECC for the error operators represented by the Kraus operators 
, with recovery operators 
Then 
is a DFS if and only if upon restriction to 
, then 
, where 
is the inverse of the system evolution operator.
In this picture of reversal of quantum operations, DFSs are a special instance of the more general QECCs whereupon restriction to a given a code, the recovery operators become proportional to the inverse of the system evolution operator, hence allowing for unitary evolution of the system.
Notice that the subtle difference between these two formulations exists in the two words preserving and correcting; in the former case, error-prevention is the method used whereas in the latter case it is error-correction. Thus the two formulations differ in that one is a passive method and the other is an active method.
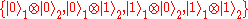which undergo collective dephasing. A random phase 
will be created between these basis qubits; therefore, the qubits will transform in the following way:
.
Under this transformation the basis states
obtain the same phase factor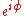 
. Thus in consideration of this, a state 
can be encoded with this information (i.e. the phase factor) and thus evolve unitarily under this dephasing process, by defining the following encoded qubits:
.
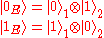Since these are basis qubits, then any state can be written as a linear combination of these states; therefore,
This state will evolve under the dephasing process as:
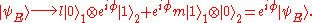
However, the overall phase for a quantum state is unobservable and, as such, is irrelevant in the description of the state. Therefore,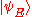
remains invariant under this dephasing process and hence the basis set 
is a decoherence-free subspace of the 4-dimensional Hilbert space. Similarly, the subspaces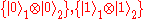 
are also DFSs.
that has a general subsystem decomposition 
The subsystem 
is a decoherence-free subsystem with respect to a system-environment coupling if every pure state in 
remains unchanged with respect to this subsystem under the OSR evolution. This is true for any possible initial condition of the environment. To understand the difference between a decoherence-free subspace and a decoherence-free subsystem, consider encoding a single qubit of information into a two-qubit system. This two-qubit system has a 4-dimensional Hilbert space; one method of encoding a single qubit into this space is by encoding information into a subspace that is spanned by two orthogonal qubits of the 4-dimensional Hilbert space. Suppose information is encoded in the orthogonal state 
in the following way:
This shows that information has been encoded into a subspace of the two-qubit Hilbert space. Another way of encoding the same information is to encode only one of the qubits of the two qubits. Suppose the first qubit is encoded, then the state of the second qubit is completely arbitrary since:
This mapping is a one-to-many mapping from the one qubit encoding information to a two-qubit Hilbert space. Instead, if the mapping is to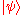
, then it is identical to a mapping from a qubit to a subspace of the two-qubit Hilbert space.
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of a system's Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
that is invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
to non-unitary
Unitarity (physics)
In quantum physics, unitarity is a restriction on the allowed evolution of quantum systems that insures the sum of probabilities of all possible outcomes of any event is always 1....
dynamics. Alternatively stated, they are a small section of the system Hilbert space where the system is decoupled
Coupling (physics)
In physics, two systems are coupled if they are interacting with each other. Of special interest is the coupling of two vibratory systems by means of springs or magnetic fields, etc...
from the environment and thus its evolution is completely unitary. DFSs can also be characterized as a special class of quantum error correcting codes. In this representation they are passive error-preventing codes since these subspaces are encoded with information that (possibly) won't require any active stabilization methods. These subspaces prevent destructive environmental interactions by isolating quantum information
Quantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
. As such, they are an important subject in quantum computing, where (coherent
Coherence (physics)
In physics, coherence is a property of waves that enables stationary interference. More generally, coherence describes all properties of the correlation between physical quantities of a wave....
) control of quantum systems is the desired goal. Decoherence
Quantum decoherence
In quantum mechanics, quantum decoherence is the loss of coherence or ordering of the phase angles between the components of a system in a quantum superposition. A consequence of this dephasing leads to classical or probabilistically additive behavior...
creates problems in this regard by causing loss of coherence between the quantum states of a system and therefore the decay of their interference
Interference
In physics, interference is a phenomenon in which two waves superpose to form a resultant wave of greater or lower amplitude. Interference usually refers to the interaction of waves that are correlated or coherent with each other, either because they come from the same source or because they have...
terms, thus leading to loss of information from the (open) quantum system to the surrounding environment. Since quantum computers cannot be isolated from their environment (i.e. we cannot have a truly isolated quantum system in the real world) and information can be lost, the study of DFSs is important for the implementation of quantum computers into the real world.
Origins
The study of DFSs began with a search for structured methods to avoid decoherence in the subject of quantum information processing (QIP). The methods involved attempted to identify particular states which have the potential of being unchanged by certain decohering processes (i.e. certain interactions with the environment). These studies started with observations made by G.M. Palma, K-A Suominen, and A.K. EkertArtur Ekert
Artur Ekert is a Professor of Quantum Physics at the Mathematical Institute, University of Oxford, and a Lee Kong Chian Centennial Professor at the National University of Singapore and also the Director of CQT...
, who studied the consequences of pure dephasing on two qubits that have the same interaction with the environment. They found that two such qubits do not decohere. Originally the term "sub-decoherence" was used by Palma to describe this situation.
Further development
Shortly afterwards, L-M Duan and G-C Guo also studied this phenomenon and reached the same conclusions as Palma, Suominen, and Ekert. However, Duan and Guo applied their own terminology, using "coherence preserving states" to describe states that do not decohere with dephasing. Duan and Guo furthered this idea of combining two qubits to preserve coherence against dephasing, to both collective dephasing and dissipation showing that decoherence is prevented in such a situation. This was shown by assuming knowledge of the system-environment coupling strength. However, such models were limited since they dealt with the decoherence processes of dephasing and dissipation solely. To deal with other types of decoherences, the previous models presented by Palma, Suominen, and Ekert, and Duan and Guo were cast into a more general setting by P. Zanardi and M. Rasetti. They expanded the existing mathematical framework to include more general system-environment interactions, such as collective decoherence-the same decoherence process acting on all the states of a quantum system and general HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
s. Their analysis gave the first formal and general circumstances for the existence of decoherence-free (DF) states, which did not rely upon knowing the system-environment coupling strength. Zanardi and Rasetti called these DF states "error avoiding codes". Subsequently, Daniel A. Lidar
Daniel Lidar
Daniel A. Lidar is a Professor of Electrical Engineering and Chemistry, and the Director and co-founder of the USC Center for Quantum Information Science & Technology , notable for his research on control of quantum systems and quantum information processing.-Education:He is class of 1986 graduate...
proposed the title "decoherence-free subspace" for the space in which these DF states exist. Lidar studied the strength of DF states against perturbation
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
s and discovered that the coherence prevalent in DF states can be upset by evolution of the system Hamiltonian. This observation discerned another prerequisite for the possible use of DF states for quantum computation. A thoroughly general requirement for the existence of DF states was obtained by Lidar, D. Bacon, and K.B. Whaley expressed in terms of the Kraus operator-sum representation (OSR).
Recent research
A subsequent development was made in generalizing the DFS picture when E. Knill, R. LaflammeRaymond Laflamme
Raymond Laflamme is a physicist and the co-founder and current director of the Institute for Quantum Computing. He is also an associate faculty member at Perimeter Institute for Theoretical Physics. He was a doctoral student of Stephen Hawking at the University of Cambridge. He is responsible for...
, and L. Viola introduced the concept of a "noiseless subsystem". Knill extended to higher-dimensional irreducible representations of the algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
generating the dynamical symmetry in the system-environment interaction. Earlier work on DFSs described DF states as singlets, which are one-dimensional irreducible representations. This work proved to be successful, as a result of this analysis was the lowering of the number of qubits required to build a DFS under collective decoherence from four to three. The generalization from subspaces to subsystems formed a foundation for combining most known decoherence prevention and nulling strategies.
Hamiltonian formulation
Consider an N-dimensional quantum system S coupled to a bath B and described by the combined system-bath Hamiltonian as follows: ,where the interaction Hamiltonian
is given in the usual way asand where
act upon the system(bath) only, and 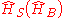is the system(bath) Hamiltonian, and is the identity operator acting on the system (bath).Under these conditions, the dynamical evolution within
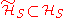, where 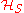is the system Hilbert space, is completely unitary 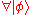(all possible bath states) if and only if:(i)
that spanLinear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
and , the space of bounded system-bath operators on 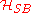,(ii) the system and bath are not coupled at first (i.e. they can be represented as a product state),
(iii) there is no "leakage" of states out of
; that is, the system Hamiltonian does not map the states out of .In other words, if the system begins in
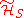(i.e. the system and bath are initially decoupled) and the system Hamiltonian leaves invariant, then is a DFS if and only if it satisfies (i).These states are degenerate
Degenerate energy levels
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
eigenkets of
and thus are distinguishable, hence preserving information in certain decohering processes. Any subspace of the system Hilbert space that satisfies the above conditions is a decoherence-free subspace. However, information can still "leak" out of this subspace if condition (iii) is not satisfied. Therefore, even if a DFS exists under the Hamiltonian conditions, there are still non-unitary actions that can act upon these subspaces and take states out of them into another subspace, which may or may not be a DFS, of the system Hilbert space.Operator-sum representation formulation
Let be an N-dimensional DFS, where is the system's (the quantum system alone) Hilbert space. The Kraus operators when written in terms of the N basis states that spanLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
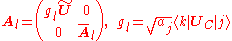
are given as:where
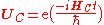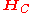( is the combined system-bath Hamiltonian), acts on 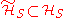, and is an arbitrary matrix that acts on 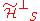(the orthogonal complement to ). Since operates on , then it will not create decoherence in ; however, it can (possibly) create decohering effects in . Consider the basis kets which span and, furthermore, they fulfill: 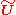is an arbitrary unitary operatorUnitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
and may or may not be time-dependent, but it is independent of the indexing variable
. The 's are complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
constants. Since
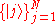spans , then any pure state can be written as a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of these basis kets:
This state will be decoherence-free; this can be seen by considering the action of
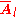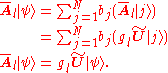
on :Therefore, in terms of the density operator representation of
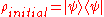, , the evolution of this state is:The above expression says that
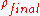is a pure state and that its evolution is unitary, since is unitary. Therefore, any state in will not decohere since its evolution is governed by a unitary operator and so its dynamical evolution will be completely unitary. Thus is a decoherence-free subspace.The above argument can be generalized to an initial arbitrary mixed state as well.
Semigroup formulation
This formulation makes use of the semigroup approach. The Lindblad decohering term determines when the dynamics of a quantum system will be unitary; in particular, when, where is the density operator representation of the state of the system, the dynamics will be decoherence-free.Let
span 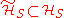, where is the system's Hilbert space. Under the assumptions that:- (i) the noise parameters of the coefficient matrix of the Lindblad decohering term are not fine-tuned (i.e. no special assumptions are made about them)
- (ii) there is no dependence on the initial conditions of the initial state of the system
a necessary and sufficient condition of for
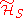to be a DFS is 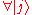:The above expression states that all basis states
are degenerate eigenstates of the error generators As such, their respective coherence terms do not decohere. Thus states within 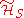will remain mutually distinguishable after a decohering process since their respective eigenvalues are degenerate and hence identifiable after action under the error generators.DFSs as a special class of information-preserving structures (IPS) and quantum error-correcting codes (QECCs)
Information-preserving structures (IPS)
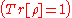DFSs can be thought of as "encoding" information through its set of states. To see this, consider a d-dimensional open quantum system that is prepared in the state-a non-negative (i.e. its eigenvalues are positive), trace-preserving , density operator that belongs to the system's Hilbert-Schmidt space, the space of bounded operatorBounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s on
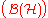. Suppose that this density operator(state) is selected from a set of states , a DFS of (the system's Hilbert space) and where .This set of states is called a code, because the states within this set encode particular kind of information; that is, the set S encodes information through its states. This information that is contained within
must be able to be accessed; since the information is encoded in the states in , these states must be distinguishable to some process, say, that attempts to acquire the information. Therefore, for two states 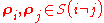, the process 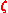is information preserving for these states if the states remain as distinguishable after the process as they were before it. Stated in a more general manner, a code 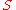(or DFS) is preserved by a process iff each pair of states is as distinguishable after is applied as they were before it was applied. A more practical description would be: is preserved by a process 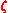if and only if and This just says that
is a 1:1 trace-distance-preserving map on . In this picture DFSs are sets of states (codes rather) whose mutual distinguishability is unaffected by a process 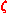.Quantum error-correcting codes(QECCs)
Since DFSs can encode information through their sets of states, then they are secure against errors (decohering processes). In this way DFSs can be looked at as a special class of QECCs, where information is encoded into states which can be disturbed by an interaction with the environment but retrieved by some reversal process.Consider a code
, which is a subspace of the system Hilbert space, with encoded information given by (i.e. the "codewords"). This code can be implemented to protect against decoherence and thus prevent loss of information in a small section of the system's Hilbert space. The errors are caused by interaction of the system with the environment (bath) and are represented by the Kraus operators. After the system has interacted with the bath, the information contained within must be able to be "decoded"; therefore, to retrieve this information a recovery operator is introduced. So a QECC is a subspace along with a set of recovery operators 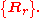Let
be a QECC for the error operators represented by the Kraus operators , with recovery operators Then is a DFS if and only if upon restriction to , then , where is the inverse of the system evolution operator.In this picture of reversal of quantum operations, DFSs are a special instance of the more general QECCs whereupon restriction to a given a code, the recovery operators become proportional to the inverse of the system evolution operator, hence allowing for unitary evolution of the system.
Notice that the subtle difference between these two formulations exists in the two words preserving and correcting; in the former case, error-prevention is the method used whereas in the latter case it is error-correction. Thus the two formulations differ in that one is a passive method and the other is an active method.
Collective dephasing
Consider a two-qubit Hilbert space, spanned by the basis qubits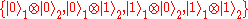 which undergo collective dephasing. A random phase will be created between these basis qubits; therefore, the qubits will transform in the following way:.Under this transformation the basis states
obtain the same phase factor 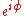. Thus in consideration of this, a state can be encoded with this information (i.e. the phase factor) and thus evolve unitarily under this dephasing process, by defining the following encoded qubits: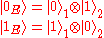.Since these are basis qubits, then any state can be written as a linear combination of these states; therefore,
This state will evolve under the dephasing process as:
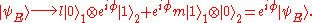
However, the overall phase for a quantum state is unobservable and, as such, is irrelevant in the description of the state. Therefore,
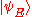remains invariant under this dephasing process and hence the basis set is a decoherence-free subspace of the 4-dimensional Hilbert space. Similarly, the subspaces 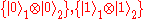are also DFSs.Alternative: decoherence-free subsystems
Consider a quantum system with an N-dimensional system Hilbert space that has a general subsystem decomposition The subsystem is a decoherence-free subsystem with respect to a system-environment coupling if every pure state in remains unchanged with respect to this subsystem under the OSR evolution. This is true for any possible initial condition of the environment. To understand the difference between a decoherence-free subspace and a decoherence-free subsystem, consider encoding a single qubit of information into a two-qubit system. This two-qubit system has a 4-dimensional Hilbert space; one method of encoding a single qubit into this space is by encoding information into a subspace that is spanned by two orthogonal qubits of the 4-dimensional Hilbert space. Suppose information is encoded in the orthogonal state in the following way:This shows that information has been encoded into a subspace of the two-qubit Hilbert space. Another way of encoding the same information is to encode only one of the qubits of the two qubits. Suppose the first qubit is encoded, then the state of the second qubit is completely arbitrary since:
This mapping is a one-to-many mapping from the one qubit encoding information to a two-qubit Hilbert space. Instead, if the mapping is to
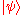, then it is identical to a mapping from a qubit to a subspace of the two-qubit Hilbert space.