The Delaunay tessellation field estimator (DTFE) is a mathematical tool for reconstructing a volume-covering and continuous density or intensity field from a discrete point set. The DTFE has various astrophysical

Astrophysics

Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...

 applications, such as the analysis of numerical simulations

Computer simulation

A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...

 of cosmic structure formation

Structure formation

Structure formation refers to a fundamental problem in physical cosmology. The universe, as is now known from observations of the cosmic microwave background radiation, began in a hot, dense, nearly uniform state approximately 13.7 Gyr ago...

, the mapping of the large scale structure in the universe and improving computer simulation programs of cosmic structure formation. It has been developed by Willem Schaap and Rien van de Weijgaert. The main advantage of the DTFE is that it automatically adapts to (strong) variations in density and geometry. It is therefore very well suited for studies of the large scale galaxy distribution.

Method

The DTFE consists of three main steps:

Step 1

The starting point is a given discrete point
distribution. In the upper left-hand frame of the figure a point distribution is plotted in which at the center of the frame an object is located whose density diminishes radially outwards. In the
first step of the DTFE the Delaunay tessellation

Delaunay triangulation

In mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...

 of the point
distribution is constructed. This is a volume-covering division
of space into triangles (tetrahedra in three dimensions), whose
vertices are formed by the point distribution (see figure, upper right-hand frame). The Delaunay tessellation is defined such
that inside the interior of the circumcircle of each Delaunay triangle
no other points from the defining point distribution are present.

Step 2

The Delaunay tessellation forms the heart of
the DTFE. In the figure it is clearly visible that the tessellation
automatically adapts to both the local density and geometry of the
point distribution: where the density is high, the triangles are small
and vice versa. The size of the triangles is therefore a measure of
the local density of the point distribution.
This property of the Delaunay tessellation is exploited in step 2 of
the DTFE, in which the local density is estimated at the locations of
the sampling points. For this purpose the density is defined at the
location of each sampling point as the inverse of the area of its
surrounding Delaunay triangles (times a normalization constant, see
figure, lower right-hand frame).

Step 3

In step 3 these density estimates are interpolated to any other point,
by assuming that inside each Delaunay triangle the density field varies
linearly (see figure, lower left-hand frame).

An atlas of the nearby universe

One of the main applications of the DTFE is the rendering of our cosmic neighborhood.
Below the DTFE reconstruction of the 2dF Galaxy Redshift Survey

2dF Galaxy Redshift Survey

In astronomy, the 2dF Galaxy Redshift Survey , 2dF or 2dFGRS is a redshift survey conducted by the Anglo-Australian Observatory with the 3.9m Anglo-Australian Telescope between 1997 and 11 April 2002. The data from this survey were made public on 30 June 2003...

 is shown, revealing
an impressive view on the cosmic structures in the nearby universe. Several superclusters

Supercluster

Superclusters are large groups of smaller galaxy groups and clusters and are among the largest known structures of the cosmos. They are so large that they are not gravitationally bound and, consequently, partake in the Hubble expansion.-Existence:...

 stand out, such as the Sloan Great Wall

Sloan Great Wall

The Sloan Great Wall is a cosmic structure formed by a giant wall of galaxies , and to the present day it is the largest known structure in the universe. Its discovery was announced on October 20, 2003 by J. Richard Gott III of Princeton University and Mario Jurić and their colleagues, based on...

, the largest structure in the universe known to date.

Numerical simulations of structure formation

Most algorithms for simulating cosmic structure formation are
particle hydrodynamics codes. At the core of these codes is the
smoothed particle hydrodynamics

Smoothed particle hydrodynamics

Smoothed-particle hydrodynamics is a computational method used for simulating fluid flows. It has been used in many fields of research, including astrophysics, ballistics, volcanology, and oceanography...

 (SPH) density estimation procedure.
Replacing it by the DTFE density estimate will yield a major
improvement for simulations incorporating feedback processes,
which play a major role in galaxy and star formation

Star formation

Star formation is the process by which dense parts of molecular clouds collapse into a ball of plasma to form a star. As a branch of astronomy star formation includes the study of the interstellar medium and giant molecular clouds as precursors to the star formation process and the study of young...

.

Cosmic velocity field

The DTFE has been designed for reconstructing density or intensity
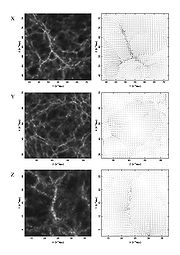
fields from a discrete set of irregularly distributed points sampling
this field. However, it can also be used to
reconstruct other continuous fields which have been sampled at the
locations of these points, for example the cosmic velocity field. The use of the DTFE for this purpose has
the same advantages as it has for reconstructing density fields. The
fields are reconstructed locally without the application of an artificial or user-dependent smoothing

Smoothing

In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. Many different algorithms are used in smoothing...

 procedure, resulting in an optimal resolution

Image resolution

Image resolution is an umbrella term that describes the detail an image holds. The term applies to raster digital images, film images, and other types of images. Higher resolution means more image detail....

 and the suppression of shot noise

Shot noise

Shot noise is a type of electronic noise that may be dominant when the finite number of particles that carry energy is sufficiently small so that uncertainties due to the Poisson distribution, which describes the occurrence of independent random events, are of significance...

effects. The
estimated quantities are volume-covering and allow for a direct
comparison with theoretical predictions.

Evolution and dynamics of the cosmic web

The DTFE has been specifically designed for describing the
complex properties of the cosmic web. It can therefore be used to study the evolution of voids and superclusters in the large scale matter galaxy distribution.

External links

• DTFE: the Delaunay Tessellation Field Estimator, Willem Schaap, 2007, PhD Thesis, Rijksuniversiteit Groningen, The Netherlands
• The Sloan Great Wall: Largest Known Structure? on APOD
• Probing cosmic velocity flows in the local universe, Emilio Romano-Diaz, 2004, PhD Thesis, Rijksuniversiteit Groningen, The Netherlands
• The cosmic web: geometric analysis, Rien van de Weygaert and Willem Schaap, 2004