Deming regression
Encyclopedia
In statistics
, Deming regression, named after W. Edwards Deming
, is an errors-in-variables model
which tries to find the line of best fit for a two-dimensional dataset. It differs from the simple linear regression
in that it accounts for errors
in observations on both the x- and the y- axis.
Deming regression is equivalent to the maximum likelihood
estimation of an errors-in-variables model
in which the errors for the two variables are assumed to be independent and normally distributed, and the ratio of their variances, denoted δ, is known. In practice, this ratio might be estimated from related data-sources; however the regression procedure takes no account for possible errors in estimating this ratio.
The Deming regression is only slightly more difficult to compute compared to the simple linear regression
. Many software packages used in clinical chemistry, such as Analyse-it
, EP Evaluator, MedCalc
and S-PLUS
offer Deming regression.
The model was originally introduced by who considered the case δ = 1, and then more generally by with arbitrary δ. However their ideas remained largely unnoticed for more than 50 years, until they were revived by and later propagated even more by . The latter book became so popular in clinical chemistry and related fields that the method was even dubbed Deming regression in those fields.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Deming regression, named after W. Edwards Deming
W. Edwards Deming
William Edwards Deming was an American statistician, professor, author, lecturer and consultant. He is perhaps best known for his work in Japan...
, is an errors-in-variables model
Errors-in-variables model
Total least squares, also known as errors in variables, rigorous least squares, or orthogonal regression, is a least squares data modeling technique in which observational errors on both dependent and independent variables are taken into account...
which tries to find the line of best fit for a two-dimensional dataset. It differs from the simple linear regression
Simple linear regression
In statistics, simple linear regression is the least squares estimator of a linear regression model with a single explanatory variable. In other words, simple linear regression fits a straight line through the set of n points in such a way that makes the sum of squared residuals of the model as...
in that it accounts for errors
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
in observations on both the x- and the y- axis.
Deming regression is equivalent to the maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimation of an errors-in-variables model
Errors-in-variables model
Total least squares, also known as errors in variables, rigorous least squares, or orthogonal regression, is a least squares data modeling technique in which observational errors on both dependent and independent variables are taken into account...
in which the errors for the two variables are assumed to be independent and normally distributed, and the ratio of their variances, denoted δ, is known. In practice, this ratio might be estimated from related data-sources; however the regression procedure takes no account for possible errors in estimating this ratio.
The Deming regression is only slightly more difficult to compute compared to the simple linear regression
Simple linear regression
In statistics, simple linear regression is the least squares estimator of a linear regression model with a single explanatory variable. In other words, simple linear regression fits a straight line through the set of n points in such a way that makes the sum of squared residuals of the model as...
. Many software packages used in clinical chemistry, such as Analyse-it
Analyse-it
Analyse-it is a statistical analysis add-in for Microsoft Excel. Analyse-it is the successor to Astute, developed in 1992 for Excel 4 and the first statistical analysis add-in for Microsoft Excel...
, EP Evaluator, MedCalc
MedCalc
MedCalc is a statistical software package designed for the biomedical sciences. It has an integrated spreadsheet for data input and can import files in several formats...
and S-PLUS
S-PLUS
S-PLUS is a commercial implementation of the S programming language sold by TIBCO Software Inc..It features object-oriented programming capabilities and advanced analytical algorithms.-Historical timeline:...
offer Deming regression.
The model was originally introduced by who considered the case δ = 1, and then more generally by with arbitrary δ. However their ideas remained largely unnoticed for more than 50 years, until they were revived by and later propagated even more by . The latter book became so popular in clinical chemistry and related fields that the method was even dubbed Deming regression in those fields.
Specification
Assume that the available data (yi, xi) are mismeasured observations of the “true” values (yi*, xi*):-
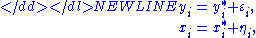
where errors ε and η are independent and the ratio of their variances is assumed to be known:
In practice the variance of the
and 
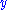parameters is often unknown which complicates the estimate of 
but where the measurement method for 
and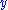 
is the same they are likely to be equal so that 
for this case.
We seek to find the line of “best fit” y* = β0 + β1x*, such that the weighted sum of squared residuals of the model is minimized:
Solution
Solution can be expressed in terms of the second-degree sample moments. That is, we first calculate the following quantities (all sums go from i = 1 to n):-
Finally, the least-squares estimates of model's parameters will be-
See also
- Errors-in-variables modelsErrors-in-variables modelsIn statistics and econometrics, errors-in-variables models or measurement errors models are regression models that account for measurement errors in the independent variables...
- Total least squares, a generalization that allows for any number of predictors and more complicated error structure
- Errors-in-variables models
-
-
