Differential inclusion
Encyclopedia
In mathematics, differential inclusions are a generalization of the concept of ordinary differential equation
of the form
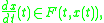
where F(t, x) is a set rather than a single point in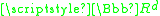
. Differential inclusions arise in many situations including differential variational inequalities
, projected dynamical system
s, dynamic Coulomb friction problems and fuzzy set
arithmetic.
For example, the basic rule for Coulomb friction is that the friction force has magnitude μN in the direction opposite to the direction of slip, where N is the normal force and μ is a constant (the friction coefficient). However, if the slip is zero, the friction force can be any force in the correct plane with magnitude smaller than or equal to μN Thus, writing the friction force as a function of position and velocity leads to a set-valued function.
Existence of solutions for the initial value problem
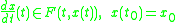
for a sufficiently small time interval [t0, t0 + ε), ε > 0 then follows.
Global existence can be shown provided F does not allow "blow-up" (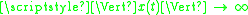
as 
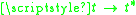for a finite 
).
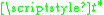Existence theory for differential inclusions with non-convex F(t, x) is an active area of research.
Uniqueness of solutions usually requires other conditions.
For example, suppose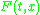
satisfies a one-sided Lipschitz condition:
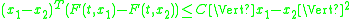
for some C for all x1 and x2. Then the initial value problem
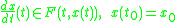
has a unique solution.
This is closely related to the theory of maximal monotone operators, as developed by Minty and Haïm Brezis
.
in the theory of differential game
s.
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
of the form
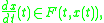
where F(t, x) is a set rather than a single point in
. Differential inclusions arise in many situations including differential variational inequalitiesDifferential variational inequality
In mathematics, a differential variational inequality is a dynamical system that incorporates ordinary differential equations and variational inequalities or complementarity problems. DVIs are useful for representing models involving both dynamics and inequality constraints...
, projected dynamical system
Projected dynamical system
Projected dynamical systems is a mathematical theory investigating the behaviour of dynamical systems where solutions are restricted to a constraint set. The discipline shares connections to and applications with both the static world of optimization and equilibrium problems and the dynamical world...
s, dynamic Coulomb friction problems and fuzzy set
Fuzzy set
Fuzzy sets are sets whose elements have degrees of membership. Fuzzy sets were introduced simultaneously by Lotfi A. Zadeh and Dieter Klaua in 1965 as an extension of the classical notion of set. In classical set theory, the membership of elements in a set is assessed in binary terms according to...
arithmetic.
For example, the basic rule for Coulomb friction is that the friction force has magnitude μN in the direction opposite to the direction of slip, where N is the normal force and μ is a constant (the friction coefficient). However, if the slip is zero, the friction force can be any force in the correct plane with magnitude smaller than or equal to μN Thus, writing the friction force as a function of position and velocity leads to a set-valued function.
Theory
Existence theory usually assumes that F(t, x) is an upper semi-continuous function of x, measurable in t, and that F(t, x) is a closed, convex set for all t and x.Existence of solutions for the initial value problem
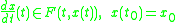
for a sufficiently small time interval [t0, t0 + ε), ε > 0 then follows.
Global existence can be shown provided F does not allow "blow-up" (
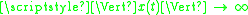as 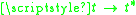for a finite 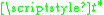).Existence theory for differential inclusions with non-convex F(t, x) is an active area of research.
Uniqueness of solutions usually requires other conditions.
For example, suppose
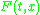satisfies a one-sided Lipschitz condition: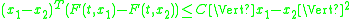for some C for all x1 and x2. Then the initial value problem
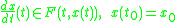
has a unique solution.
This is closely related to the theory of maximal monotone operators, as developed by Minty and Haïm Brezis
Haïm Brezis
Haïm Brezis is a French mathematician who works in functional analysis and partial differential equations.Born in Riom-ès-Montagnes, Cantal, France. Brezis is the son of Romanian immigrant father, who came to France in the 1930s, and his mother is a Jew who fled from Holland...
.
Applications
Differential inclusions can be used to understand and suitably interpret discontinuous ordinary differential equations, such as arise for Coulomb friction in mechanical systems and ideal switches in power electronics. An important contribution has been made by Filippov, who studied regularizations of discontinuous equations. Further the technique of regularization was used by KrasovskiiNikolai Nikolaevich Krasovsky
Nikolay Nikolayevich Krasovsky is a prominent Russian mathematician who works in the mathematical theory of control, the theory of dynamical systems, and the theory of differential games...
in the theory of differential game
Differential game
In game theory, differential games are a group of problems related to the modeling and analysis of conflict in the context of a dynamical system. The problem usually consists of two actors, a pursuer and an evader, with conflicting goals...
s.