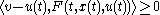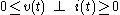Differential variational inequality
Encyclopedia
In mathematics, a differential variational inequality (DVI) is a dynamical system
that incorporates ordinary differential equation
s and variational inequalities
or complementarity problems
. DVIs are useful for representing models involving both dynamics and inequality constraints. Examples of such problems include, for example, mechanical impact problems, electrical circuits with ideal diode
s, Coulomb friction problems for contacting bodies, and dynamic economic and related problems such as dynamic traffic networks and networks of queues (where the constraints can either be upper limits on queue length or that the queue length cannot become negative). DVIs are related to a number of other concepts including differential inclusions, projected dynamical systems, evolutionary inequalities, and parabolic variational inequalities.
Differential variational inequalities were first formally introduced by Pang
and Stewart
, whose definition should not be confused with the differential variational inequality used in Aubin and Cellina (1984).
Differential variational inequalities have the form to find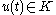
such that
for every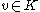
and almost all t; K a closed convex set, where
Closely associated with DVIs are dynamic/differential complementarity problems: if K is a closed convex cone, then the variational inequality is equivalent to the complementarity problem:
falling from a height towards a table. Assume that the forces acting on the ball are gravitation and the contact forces of the table preventing penetration. Then the differential equation describing the motion is
where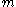
is the mass of the ball and 
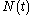is the contact force of the table, and 
is the gravitational acceleration. Note that both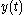 
and 
are a priori unknown. While the ball and the table are separated, there is no contact force. There cannot be penetration (for a rigid ball and a rigid table), so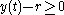 
for all 
. If 
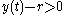then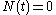 
. On the other hand, if 
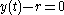, then 
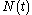can take on any non-negative value. (We do not allow 
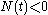as this corresponds to some kind of adhesive.) This can be summarized by the complementarity relationship
In the above formulation, we can set
, so that its dual cone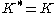 
is also the set of non-negative real numbers; this is a differential complementarity problem.
, and the forward current is 
, then there is a complementarity relationship between the two:
for all
. If the diode is in a circuit containing a memory element, such as a capacitor or inductor, then the circuit can be represented as a differential variational inequality.
This index can be computed for the above examples. For the mechanical impact example, if we differentiate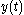
once we have 
, which does not yet explicitly involve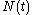 
. However, if we differentiate once more, we can use the differential equation to give 
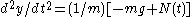, which does explicitly involve 
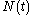. Furthermore, if 
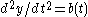, we can explicitly determine 
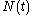in terms of 
.
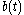For the ideal diode systems, the computations are considerably more difficult, but provided some generally valid conditions hold, the differential variational inequality can be shown to have index one.
Differential variational inequalities with index greater than two are generally not meaningful, but certain conditions and interpretations can make them meaningful (see the references Acary, Brogliato and Goeleven, and Heemels, Schumacher, and Weiland below).
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
that incorporates ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s and variational inequalities
Variational inequality
In mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all the value of a given variable, belonging usually to a convex set...
or complementarity problems
Complementarity theory
A complementarity problem is a type of mathematical optimization problem. It is the problem of optimizing a function of two vector variables subject to certain requirements which include: that the inner product of the two variables must equal zero, i.e. = 0...
. DVIs are useful for representing models involving both dynamics and inequality constraints. Examples of such problems include, for example, mechanical impact problems, electrical circuits with ideal diode
Diode
In electronics, a diode is a type of two-terminal electronic component with a nonlinear current–voltage characteristic. A semiconductor diode, the most common type today, is a crystalline piece of semiconductor material connected to two electrical terminals...
s, Coulomb friction problems for contacting bodies, and dynamic economic and related problems such as dynamic traffic networks and networks of queues (where the constraints can either be upper limits on queue length or that the queue length cannot become negative). DVIs are related to a number of other concepts including differential inclusions, projected dynamical systems, evolutionary inequalities, and parabolic variational inequalities.
Differential variational inequalities were first formally introduced by Pang
Pang
-People:*Includes name origin of the alternate romanization of Peng*Pang Juan , military general from the Warring States Period*Pang Tong , strategist and advisor from the late Han Dynasty*Pang Wanchun , fictional character from Water Margin...
and Stewart
Stewart
Stewart is a popular Scottish given name and surname. The word Stewart is derived from an occupational surname. It originally belonged to a person who was a steward by profession. It is derived from a combination of two Old English words, the word stig, which means house, and the word weard, which...
, whose definition should not be confused with the differential variational inequality used in Aubin and Cellina (1984).
Differential variational inequalities have the form to find
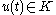such that
for every
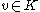and almost all t; K a closed convex set, where
Closely associated with DVIs are dynamic/differential complementarity problems: if K is a closed convex cone, then the variational inequality is equivalent to the complementarity problem:
Mechanical Contact
Consider a rigid ball of radius falling from a height towards a table. Assume that the forces acting on the ball are gravitation and the contact forces of the table preventing penetration. Then the differential equation describing the motion is
where
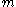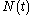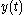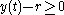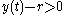is the mass of the ball and is the contact force of the table, and is the gravitational acceleration. Note that both and are a priori unknown. While the ball and the table are separated, there is no contact force. There cannot be penetration (for a rigid ball and a rigid table), so for all . If then 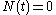. On the other hand, if 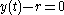, then 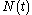can take on any non-negative value. (We do not allow 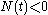as this corresponds to some kind of adhesive.) This can be summarized by the complementarity relationship
In the above formulation, we can set
, so that its dual cone 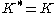is also the set of non-negative real numbers; this is a differential complementarity problem.Ideal diodes in electrical circuits
An ideal diode is a diode that conducts electricity in the forward direction with no resistance if a forward voltage is applied, but allows no current to flow in the reverse direction. Then if the reverse voltage is, and the forward current is , then there is a complementarity relationship between the two:
for all
. If the diode is in a circuit containing a memory element, such as a capacitor or inductor, then the circuit can be represented as a differential variational inequality.Index
The concept of the index of a DVI is important and determines many questions of existence and uniqueness of solutions to a DVI. This concept is closely related to the concept of index for differential algebraic equations (DAE's), which is the number of times the algebraic equations of a DAE must be differentiated in order to obtain a complete system of differential equations for all variables. For a DVI, the index is the number of differentiations of F(t, x, u) = 0 needed in order to locally uniquely identify u as a function of t and x.This index can be computed for the above examples. For the mechanical impact example, if we differentiate
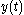once we have , which does not yet explicitly involve 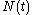. However, if we differentiate once more, we can use the differential equation to give 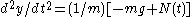, which does explicitly involve 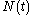. Furthermore, if 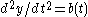, we can explicitly determine 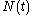in terms of 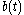.For the ideal diode systems, the computations are considerably more difficult, but provided some generally valid conditions hold, the differential variational inequality can be shown to have index one.
Differential variational inequalities with index greater than two are generally not meaningful, but certain conditions and interpretations can make them meaningful (see the references Acary, Brogliato and Goeleven, and Heemels, Schumacher, and Weiland below).
See also
- Variational inequalityVariational inequalityIn mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all the value of a given variable, belonging usually to a convex set...
- Complementarity problem
- Projected dynamical systems
- Differential inclusion