Direct numerical simulation
Encyclopedia
A direct numerical simulation (DNS) is a simulation
in computational fluid dynamics
in which the Navier-Stokes equations
are numerically solved without any turbulence
model. This means that the whole range of spatial and temporal
scales of the turbulence must be resolved.
All the spatial scales of the turbulence must be resolved in the computational mesh, from the smallest dissipative scales (Kolmogorov microscales
), up to the integral scale L, associated with the motions containing most of the kinetic energy. The Kolmogorov scale,
, is given by
where ν is the kinematic viscosity
and ε is the rate of kinetic energy
dissipation. On the other hand, the integral scale depends usually on the spatial scale of the boundary conditions.
To satisfy these resolution requirements, the number N of points along a given mesh direction with increments h, must be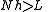
,
so that the integral scale is contained within the computational domain, and also
,
so that the Kolmogorov scale can be resolved.
Since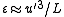
,
where u is the root mean square
(RMS) of the velocity
, the previous relations imply that a three-dimensional DNS requires a number of mesh points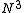
satisfying
where Re is the turbulent Reynolds number: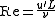
.
Hence, the memory storage requirement in a DNS grows very fast with the Reynolds number. In addition, given the very large memory necessary, the integration of the solution in time must be done by an explicit method. This means that in order to be accurate, the integration must be done with a time step, Δt, small enough such that a fluid particle moves only a fraction of the mesh spacing h in each step. That is,
(C is here the Courant number). The total time interval simulated is generally proportional to the turbulence time scale
given by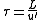
.
Combining these relations, and the fact that h must be of the order of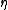
, the number of time-integration steps must be proportional to 
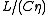. By other hand, from the definitions for Re, η and L given above, it follows that
,
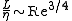and consequently, the number of time steps grows also as a power law of the Reynolds number.
One can estimate that the number of floating-point operations required to complete the simulation is proportional to the number of mesh points and the number of time steps, and in conclusion, the number of operations grows as Re3.
Therefore, the computational cost of DNS is very high, even at low Reynolds numbers. For the Reynolds numbers encountered in most industrial applications, the computational resources required by a DNS would exceed the capacity of the most powerful computers currently available
. However, direct numerical simulation is a useful tool in fundamental research in turbulence. Using DNS it is possible to perform "numerical experiments", and extract from them information difficult or impossible to obtain in the laboratory, allowing a better understanding of the physics of turbulence. Also, direct numerical simulations are useful in the development of turbulence models for practical applications, such as sub-grid scale models for Large eddy simulation
(LES) and models for methods that solve the Reynolds-averaged Navier-Stokes equations
(RANS). This is done by means of "a priori" tests, in which the input data for the model is taken from a DNS simulation, or by "a posteriori" tests, in which the results produced by the model are compared with those obtained by DNS. The biggest DNS in the world, up to this date, used 40963 mesh points. It was carried out in the Japanese Earth Simulator
supercomputer in 2002.
Simulation
Simulation is the imitation of some real thing available, state of affairs, or process. The act of simulating something generally entails representing certain key characteristics or behaviours of a selected physical or abstract system....
in computational fluid dynamics
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
in which the Navier-Stokes equations
Navier-Stokes equations
In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
are numerically solved without any turbulence
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
model. This means that the whole range of spatial and temporal
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
scales of the turbulence must be resolved.
All the spatial scales of the turbulence must be resolved in the computational mesh, from the smallest dissipative scales (Kolmogorov microscales
Kolmogorov microscales
Kolmogorov microscales are the smallest scales in turbulent flow. They are defined bywhere \epsilon is the average rate of energy dissipation per unit mass, and \nu is the kinematic viscosity of the fluid....
), up to the integral scale L, associated with the motions containing most of the kinetic energy. The Kolmogorov scale,
, is given bywhere ν is the kinematic viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
and ε is the rate of kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
dissipation. On the other hand, the integral scale depends usually on the spatial scale of the boundary conditions.
To satisfy these resolution requirements, the number N of points along a given mesh direction with increments h, must be
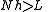,so that the integral scale is contained within the computational domain, and also
,so that the Kolmogorov scale can be resolved.
Since
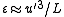,where u is the root mean square
Root mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
(RMS) of the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, the previous relations imply that a three-dimensional DNS requires a number of mesh points
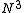satisfyingwhere Re is the turbulent Reynolds number:
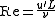.Hence, the memory storage requirement in a DNS grows very fast with the Reynolds number. In addition, given the very large memory necessary, the integration of the solution in time must be done by an explicit method. This means that in order to be accurate, the integration must be done with a time step, Δt, small enough such that a fluid particle moves only a fraction of the mesh spacing h in each step. That is,
(C is here the Courant number). The total time interval simulated is generally proportional to the turbulence time scale
given by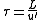.Combining these relations, and the fact that h must be of the order of
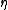, the number of time-integration steps must be proportional to 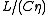. By other hand, from the definitions for Re, η and L given above, it follows that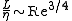,and consequently, the number of time steps grows also as a power law of the Reynolds number.
One can estimate that the number of floating-point operations required to complete the simulation is proportional to the number of mesh points and the number of time steps, and in conclusion, the number of operations grows as Re3.
Therefore, the computational cost of DNS is very high, even at low Reynolds numbers. For the Reynolds numbers encountered in most industrial applications, the computational resources required by a DNS would exceed the capacity of the most powerful computers currently available
Supercomputer
A supercomputer is a computer at the frontline of current processing capacity, particularly speed of calculation.Supercomputers are used for highly calculation-intensive tasks such as problems including quantum physics, weather forecasting, climate research, molecular modeling A supercomputer is a...
. However, direct numerical simulation is a useful tool in fundamental research in turbulence. Using DNS it is possible to perform "numerical experiments", and extract from them information difficult or impossible to obtain in the laboratory, allowing a better understanding of the physics of turbulence. Also, direct numerical simulations are useful in the development of turbulence models for practical applications, such as sub-grid scale models for Large eddy simulation
Large eddy simulation
Large eddy simulation is a mathematical model for turbulence used in computational fluid dynamics. It was initially proposed in 1963 by Joseph Smagorinsky to simulate atmospheric air currents, and many of the issues unique to LES were first explored by Deardorff...
(LES) and models for methods that solve the Reynolds-averaged Navier-Stokes equations
Reynolds-averaged Navier-Stokes equations
The Reynolds-averaged Navier–Stokes equations are time-averagedequations of motion for fluid flow. The idea behind the equations is Reynolds decomposition, whereby an instantaneous quantity is decomposed into its time-averaged and fluctuating quantities, an idea first proposed by Osborne Reynolds...
(RANS). This is done by means of "a priori" tests, in which the input data for the model is taken from a DNS simulation, or by "a posteriori" tests, in which the results produced by the model are compared with those obtained by DNS. The biggest DNS in the world, up to this date, used 40963 mesh points. It was carried out in the Japanese Earth Simulator
Earth Simulator
The Earth Simulator , developed by the Japanese government's initiative "Earth Simulator Project", was a highly parallel vector supercomputer system for running global climate models to evaluate the effects of global warming and problems in solid earth geophysics...
supercomputer in 2002.
External links
- DNS page at CFD-Wiki