
Director circle
Encyclopedia
In geometry
, the director circle of an ellipse
or hyperbola
(also called the orthoptic
circle or Fermat–Apollonius circle) is a circle
formed by the points where two perpendicular
tangent lines to the curve cross.
The director circle of an ellipse circumscribes
the minimum bounding box
of the ellipse. It has the same center as the ellipse, with radius √(a2 + b2), where a and b are the semi-major axis
and semi-minor axis
of the ellipse. Additionally, it has the property that, when viewed from any point on the circle, the ellipse spans a right angle
.
More generally, for any collection of points Pi, weights wi, and constant C, one can define a circle as the locus of points X such that
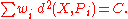
The director circle of an ellipse is a special case of this more general construction with two points P1 and P2 at the foci of the ellipse, weights w1 = w2 = 1, and C equal to the square of the major axis of the ellipse. The Apollonius circle, the locus of points X such that the ratio of distances of X to two foci P1 and P1 is a fixed constant r, is another special case, with w1 = 1, w2 = −r2, and C = 0.
In the case of a parabola
the director circle degenerates to a straight line, the directrix of the parabola.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the director circle of an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
or hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
(also called the orthoptic
Isoptic
In the geometry of curves, an isoptic is the set of points for which two tangents of a given curve meet at a given angle. The orthoptic is the isoptic whose given angle is a right angle....
circle or Fermat–Apollonius circle) is a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
formed by the points where two perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
tangent lines to the curve cross.
The director circle of an ellipse circumscribes
Circumscribed circle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
the minimum bounding box
Minimum bounding box
The minimum or smallest bounding or enclosing box for a point set in N dimensions is the box with the smallest measure within which all the points lie...
of the ellipse. It has the same center as the ellipse, with radius √(a2 + b2), where a and b are the semi-major axis
Semi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
and semi-minor axis
Semi-minor axis
In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...
of the ellipse. Additionally, it has the property that, when viewed from any point on the circle, the ellipse spans a right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
.
More generally, for any collection of points Pi, weights wi, and constant C, one can define a circle as the locus of points X such that
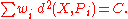
The director circle of an ellipse is a special case of this more general construction with two points P1 and P2 at the foci of the ellipse, weights w1 = w2 = 1, and C equal to the square of the major axis of the ellipse. The Apollonius circle, the locus of points X such that the ratio of distances of X to two foci P1 and P1 is a fixed constant r, is another special case, with w1 = 1, w2 = −r2, and C = 0.
In the case of a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
the director circle degenerates to a straight line, the directrix of the parabola.

