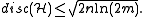Hypergraph discrepancies in two colors

In the classical setting, we aim at partitioning the vertices

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

 of a hypergraph

Hypergraph

In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...

 into two classes in such a way that ideally each hyperedge contains the same number of vertices in both classes. A partition into two classes can be represented by a coloring 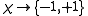. We call -1 and +1 colors. The color-classes and 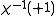form the corresponding partition. For a hyperedge 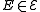, set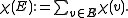
The discrepancy of 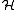with respect to 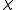and the discrepancy of 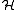are defined by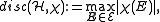
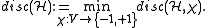
These notions as well as the term 'discrepancy' seem to have appeared fo the first time in a paper of Beck

József Beck

József Beck is a Harold H. Martin Professor of Mathematics at Rutgers University.His contributions to combinatorics include the partial colouring lemma and the Beck–Fiala theorem in discrepancy theory, the algorithmic version of the Lovász local lemma, the two extremes theorem in combinatorial...

. Earlier results on this problem include the famous lower bound on the discrepancy of arithmetic progressions by Roth and upper bounds for this problem and other results by Erdős

Paul Erdos

Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...

 and Spencer and Sárközi (described on p. 39 ). At that time, discrepancy problems were called quasi-Ramsey

Ramsey theory

Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...

 problems.

To get some intuition for this concept, let's have a look at a few examples.

• If all edges of intersect trivially, i.e. 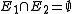for any two distinct edges 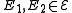, then the discrepancy is zero, if all edges have even cardinality, and one, if there is an odd cardinality edge.
• The other extreme is marked by the complete hypergraph 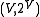. In this case the discrepancy is 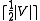. Any 2-coloring will have a color class of at least this size, and this set is also an edge. On the other hand, any coloring 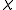with color classes of size and 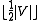proves that the discrepancy is not larger than 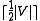. It seems that the discrepancy reflects how chaotic the hyperedges of 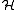intersect. Things are not that easy, however, as the following example shows.
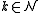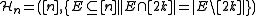• Set , and . Now 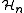has many (more than 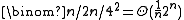) complicatedly intersecting edges, but discrepancy zero.

The last example shows that we cannot expect to determine the discrepancy by looking at a single parameter like the number of hyperedges. Still, the size of the hypergraph yields first upper bounds.

Theorems

• 

with n the number of vertices and m the number of edges.

The proof is a simple application of the probabilistic method:
Let 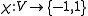be a random coloring, i.e. we have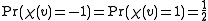
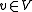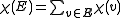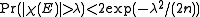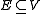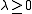independently for all . Since is a sum of independent -1, 1 random variables. So we have for all and . Put 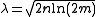for convenience. Then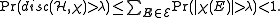
Since a random coloring with positive probability has discrepancy at most 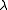, in particular, there are colorings that have discrepancy at most 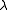. Hence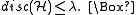

• For any hypergraph 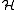such that 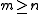we have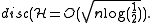

To prove this, a much more sophisticated approach using the entropy function was necessary.
Of course this particularly interesting for 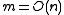. In the case , 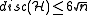can be shown for n large enough. Therefore, this result is usually known to as 'Six Standard Deviations Suffics'. It is considered to be one of the milestones of discrepancy theory. The entropy method has seen numerous other applications, e. g. in the proof of the tight upper bound for the arithmetic progressions of Matoušek

Jirí Matoušek (mathematician)

Jiří Matoušek is a Czech mathematician working in computational geometry. He is a professor at Charles University in Prague and is the author of several textbooks and research monographs....

 and Spencer or the upper bound in terms of the primal shatter function due to Matoušek.

• Assume that each vertex of 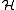is contained in at most t edges. Then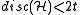

This beautiful result is due to Beck and Fiala. They bound the discrepancy by the maximum degree of .
It is a famous open problem whether this bound can be improved or not. Beck and Fiala conjectured that 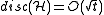, but little progress has been made so far in this direction. Bednarchak and Helm and Helm improved the Beck-Fiala bound in tiny steps to 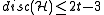(for a slightly restricted situation, i.e. 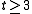). A corollary of Beck's paper - the first time the notion of discrepancy explicitly appeared - shows 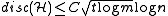for some constant C. The latest improvement in this direction is due to Banaszczyk: .

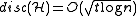Classic theorems

• Axis-parallel rectangles in the plane (Roth
  Klaus Roth
  Klaus Friedrich Roth is a British mathematician known for work on diophantine approximation, the large sieve, and irregularities of distribution. He was born in Breslau, Prussia, but raised and educated in the UK. He graduated from Peterhouse, Cambridge in 1945...
  
  , Schmidt)
• Discrepancy of half-planes (Alexander, Matoušek)
• Arithmetic progressions (Roth, Sárközy, Beck
  József Beck
  József Beck is a Harold H. Martin Professor of Mathematics at Rutgers University.His contributions to combinatorics include the partial colouring lemma and the Beck–Fiala theorem in discrepancy theory, the algorithmic version of the Lovász local lemma, the two extremes theorem in combinatorial...
  
  , Matoušek & Spencer
  Joel Spencer
  Joel Spencer is an American mathematician. He is a combinatorialist who has worked on probabilistic methods in combinatorics and on Ramsey theory. He received his doctorate from Harvard University in 1970, under the supervision of Andrew Gleason...
  
  )
• Beck-Fiala theorem
• Six Standard Deviations Suffice (Spencer)

Major open problems

• Axis-parallel rectangles in dimensions three and higher (Folklore)
• Komlos conjecture
• The three permutations problem (Beck)
• Homogeneous arithmetic progressions (Erdős
  Paul Erdos
  Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
  
  , $500)

Applications

• Numerical Integration: Monte Carlo methods in high dimensions.
• Computational Geometry: Divide and conquer algorithms.
• Image Processing: Halftoning