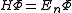Discrete delta-potential method
Encyclopedia
The discrete delta potential method is a combination of both numerical and analytic method used to solve the Schrödinger equation
the main feature of this method is to obtain first a discrete approximation of the potential in the form:
where the i index runs over several discrete chosen points of the continuous potential, with this we can solve the SE in the form:
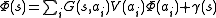
Where G(s, r) is the Green function
associated to the free particle Hamiltonian H0, setting s=ai for every i would give a system of linear equation.
For a better approach if potential V(x) is weak we can treat the continuous part of the potential and perform perturbation theory
to obtain a better wave function.
If the points are equidistant :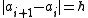
the wave function will depend on h so performing the solution to several h and extrapolating to the value h=0 we could obtain the solution of SE (Schrödinger equation).
This method is valuable when we cannot perform perturbation theory and need some analytic approach to the solution of SE: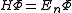
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
the main feature of this method is to obtain first a discrete approximation of the potential in the form:
where the i index runs over several discrete chosen points of the continuous potential, with this we can solve the SE in the form:
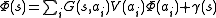
Where G(s, r) is the Green function
Green function
Green function might refer to:*Green's function of a differential operator.*Deligne–Lusztig theory in the representation theory of finite groups of Lie type.*Green's function in many-body theory....
associated to the free particle Hamiltonian H0, setting s=ai for every i would give a system of linear equation.
For a better approach if potential V(x) is weak we can treat the continuous part of the potential and perform perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
to obtain a better wave function.
If the points are equidistant :
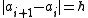the wave function will depend on h so performing the solution to several h and extrapolating to the value h=0 we could obtain the solution of SE (Schrödinger equation).This method is valuable when we cannot perform perturbation theory and need some analytic approach to the solution of SE: