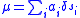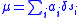Discrete measure
Encyclopedia
In mathematics
, more precisely in measure theory, a measure
on the real line
is called a discrete measure (in respect to the Lebesgue measure
) if its support
is at most a countable set
. Note that the support need not be a discrete set. Geometrically, a discrete measure (on the real line, with respect to Lebesgue measure) is a collection of point masses.
defined on the Lebesgue measurable set
s of the real line with values in
is said to be discrete if there exists a (possibly finite) sequence
of numbers
such that
The simplest example of a discrete measure on the real line is the Dirac delta function
One has 
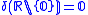and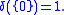 
More generally, if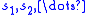
is a (possibly finite) sequence of real numbers, 
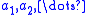is a sequence of numbers in 
of the same length, one can consider the Dirac measures 
defined by
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more precisely in measure theory, a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
is called a discrete measure (in respect to the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
) if its support
Support (measure theory)
In mathematics, the support of a measure μ on a measurable topological space is a precise notion of where in the space X the measure "lives"...
is at most a countable set
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
. Note that the support need not be a discrete set. Geometrically, a discrete measure (on the real line, with respect to Lebesgue measure) is a collection of point masses.
Definition and properties
A measure defined on the Lebesgue measurable setLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
s of the real line with values in
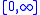is said to be discrete if there exists a (possibly finite) sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of numbers
such that
The simplest example of a discrete measure on the real line is the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
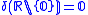One has and 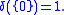More generally, if
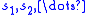is a (possibly finite) sequence of real numbers, 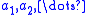is a sequence of numbers in 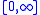of the same length, one can consider the Dirac measures defined by-
for any Lebesgue measurable set
Then, the measure
is a discrete measure. In fact, one may prove that any discrete measure on the real line has this form for appropriately chosen sequences
and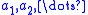 
Extensions
One may extend the notion of discrete measures to more general measure spaces. Given a measure space
and two measures 
and 
on it, 
is said to be discrete in respect to 
if there exists an at most countable subset 
of 
such that
- All singletons
with 
in 
are measurable (which implies that any subset of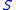 
is measurable) -
-
Notice that the first two requirements are always satisfied for an at most countable subset of the real line if
is the Lebesgue measure, so they were not necessary in the first definition above.
As in the case of measures on the real line, a measure
on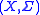 
is discrete in respect to another measure 
on the same space if and only if 
has the form
where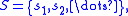
the singletons 
are in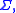 
and their 
measure is 0.
One can also define the concept of discreteness for signed measureSigned measureIn mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
s. Then, instead of conditions 2 and 3 above one should ask that
be zero on all measurable subsets of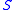 
and 
be zero on measurable subsets of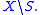 
-
