Discrete phase-type distribution
Encyclopedia
The discrete phase-type distribution is a probability distribution that results from a system of one or more inter-related geometric distributions occurring in sequence, or phases. The sequence in which each of the phases occur may itself be a stochastic process
. The distribution can be represented by a random variable describing the time until absorption of an absorbing Markov chain
with one absorbing state. Each of the states of the Markov chain represents one of the phases.
It has continuous time equivalent in the phase-type distribution
.
where all states are transient, except one which is absorbing.
Reordering the states, the transition probability matrix of a terminating Markov chain with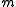
transient states is
where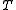
is a 
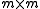matrix and 
. The transition matrix is characterized entirely by its upper-left block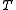 
.
Definition. A distribution on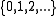
is a discrete phase-type distribution if it is the distribution of the first passage time to the absorbing state of a terminating Markov chain with finitely many states.
the upper-left block of its transition matrix and 
the initial distribution.
The distribution of the first time to the absorbing state is denoted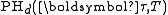
or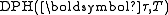 
.
Its cumulative distribution function is
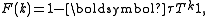
for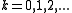
, and its density function is
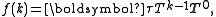
for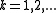
. It is assumed the probability of process starting in the absorbing state is zero. The factorial moments of the distribution function are given by,
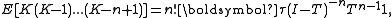
where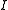
is the appropriate dimension identity matrix
.
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
. The distribution can be represented by a random variable describing the time until absorption of an absorbing Markov chain
Absorbing Markov chain
In the mathematical theory of probability, an absorbing Markov chain is a Markov chain in which every state can reach an absorbing state. An absorbing state is a state that, once entered, cannot be left....
with one absorbing state. Each of the states of the Markov chain represents one of the phases.
It has continuous time equivalent in the phase-type distribution
Phase-type distribution
A phase-type distribution is a probability distribution that results from a system of one or more inter-related Poisson processes occurring in sequence, or phases. The sequence in which each of the phases occur may itself be a stochastic process. The distribution can be represented by a random...
.
Definition
A terminating Markov chain is a Markov chainMarkov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
where all states are transient, except one which is absorbing.
Reordering the states, the transition probability matrix of a terminating Markov chain with
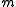transient states iswhere
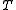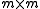is a matrix and . The transition matrix is characterized entirely by its upper-left block 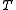.Definition. A distribution on
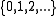is a discrete phase-type distribution if it is the distribution of the first passage time to the absorbing state of a terminating Markov chain with finitely many states.Characterization
Fix a terminating Markov chain. Denote the upper-left block of its transition matrix and the initial distribution.The distribution of the first time to the absorbing state is denoted
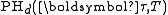or 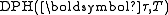.Its cumulative distribution function is
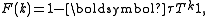
for
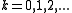, and its density function is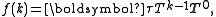for
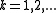. It is assumed the probability of process starting in the absorbing state is zero. The factorial moments of the distribution function are given by,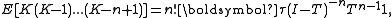where
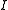is the appropriate dimension identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
Special cases
Just as the continuous time distribution is a generalisation of the exponential distribution, the discrete time distribution is a generalisation of the geometric distribution, for example:- Degenerate distribution, point mass at zero or the empty phase-type distribution - 0 phases.
- Geometric distribution - 1 phase.
- Negative binomial distributionNegative binomial distributionIn probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
- 2 or more identical phases in sequence. - Mixed Geometric distribution- 2 or more non-identical phases, that each have a probability of occurring in a mutually exclusive, or parallel, manner. This is the discrete analogue of the Hyperexponential distribution, but it is not called the Hypergeometric distribution, since that name is in use for an entirely different type of discrete distribution.