
Divided power structure
Encyclopedia
In mathematics
, specifically commutative algebra
, a divided power structure is a way of making expressions of the form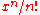 meaningful even when it is not possible to actually divide by
meaningful even when it is not possible to actually divide by  .
.
with an ideal
I. A divided power structure (or PD-structure, after the French puissances divisées) on I is a collection of maps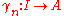 for n=0, 1, 2, ... such that:
for n=0, 1, 2, ... such that:
For convenience of notation,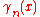 is often written as
is often written as  when it is clear what divided power structure is meant.
when it is clear what divided power structure is meant.
The term divided power ideal refers to an ideal with a given divided power structure, and divided power ring refers to a ring with a given ideal with divided power structure.

consisting of divided power polynomials in the variables

that is sums of divided power monomials of the form

with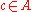 . Here the divided power ideal is the set of divided power polynomials with constant coefficient 0.
. Here the divided power ideal is the set of divided power polynomials with constant coefficient 0.
More generally, if M is an A-module, there is a universal A-algebra, called
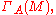
with PD ideal
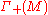
and an A-linear map
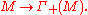
(The case of divided power polynomials is the special case in which M is a free module
over A of finite rank.)
If I is any ideal of a ring A, there is a universal construction which extends A with divided powers of elements of I to get a divided power envelope of I in A.
, where it is used to overcome technical difficulties which arise in positive characteristic
.
The divided power functor is used in the construction of co-Schur functors.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, a divided power structure is a way of making expressions of the form
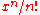 meaningful even when it is not possible to actually divide by
meaningful even when it is not possible to actually divide by  .
.Definition
Let A be a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
with an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
I. A divided power structure (or PD-structure, after the French puissances divisées) on I is a collection of maps
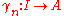 for n=0, 1, 2, ... such that:
for n=0, 1, 2, ... such that: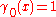 and
and 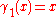 for
for 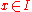 , while
, while 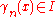 for n > 0.
for n > 0. for
for 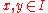 .
.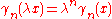 for
for  .
.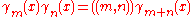 for
for 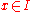 , where
, where 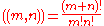 is an integer.
is an integer. for
for 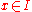 , where
, where  is an integer.
is an integer.
For convenience of notation,
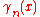 is often written as
is often written as  when it is clear what divided power structure is meant.
when it is clear what divided power structure is meant.The term divided power ideal refers to an ideal with a given divided power structure, and divided power ring refers to a ring with a given ideal with divided power structure.
Examples
- If A is an algebra over the rational numbers Q, then every ideal I has a unique divided power structure where
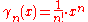 . (The uniqueness follows from the easily verified fact that in general,
. (The uniqueness follows from the easily verified fact that in general, 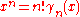 .) Indeed, this is the example which motivates the definition in the first place.
.) Indeed, this is the example which motivates the definition in the first place.
- If A is a ring of characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
 , where p is prime, and I is an ideal such that
, where p is prime, and I is an ideal such that 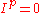 , then we can define a divided power structure on I where
, then we can define a divided power structure on I where 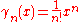 if n < p, and
if n < p, and 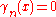 if
if  . (Note the distinction between
. (Note the distinction between 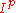 and the ideal generated by
and the ideal generated by  for
for 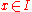 ; the latter is always zero if a divided power structure exists, while the former is not necessarily zero.)
; the latter is always zero if a divided power structure exists, while the former is not necessarily zero.)
- If M is an A-module, let
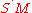 denote the symmetric algebraSymmetric algebraIn mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
denote the symmetric algebraSymmetric algebraIn mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
of M over A. Then its dual has a canonical structure of divided power ring. In fact, it is canonically isomorphic to a natural completionComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
has a canonical structure of divided power ring. In fact, it is canonically isomorphic to a natural completionComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
of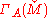 (see below) if M has finite rank.
(see below) if M has finite rank.
Constructions
If A is any ring, there exists a divided power ring
consisting of divided power polynomials in the variables

that is sums of divided power monomials of the form

with
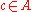 . Here the divided power ideal is the set of divided power polynomials with constant coefficient 0.
. Here the divided power ideal is the set of divided power polynomials with constant coefficient 0.More generally, if M is an A-module, there is a universal A-algebra, called
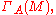
with PD ideal
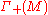
and an A-linear map
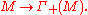
(The case of divided power polynomials is the special case in which M is a free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
over A of finite rank.)
If I is any ideal of a ring A, there is a universal construction which extends A with divided powers of elements of I to get a divided power envelope of I in A.
Applications
The divided power envelope is a fundamental tool in the theory of PD differential operators and crystalline cohomologyCrystalline cohomology
In mathematics, crystalline cohomology is a Weil cohomology theory for schemes introduced by and developed by . Its values are modules over rings of Witt vectors over the base field....
, where it is used to overcome technical difficulties which arise in positive characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
.
The divided power functor is used in the construction of co-Schur functors.

