
Crystalline cohomology
Encyclopedia
In mathematics, crystalline cohomology is a Weil cohomology theory
for schemes introduced by and developed by . Its values are modules over rings of Witt vector
s over the base field.
Crystalline cohomology is partly inspired by the p-adic proof in of part of the Weil conjectures
and is closely related to the (algebraic) de Rham cohomology introduced by Grothendieck (1963). Roughly speaking, crystalline cohomology of a variety X in characteristic p is the de Rham cohomology of a smooth lift of X to characteristic 0, while de Rham cohomology of X is the crystalline cohomology reduced mod p (after taking into account higher Tors).
The idea of crystalline cohomology, roughly, is to replace the Zariski open sets of a scheme by infinitesimal thickenings of Zariski open sets with divided power structure
s. The motivation for this is that it can then be calculated by taking a local lifting of a scheme from characteristic p to characteristic 0 and employing an appropriate version of algebraic de Rham cohomology.
Crystalline cohomology only works well for smooth proper schemes. Rigid cohomology
extends it to more general schemes.
s.
Crystalline cohomology, from the point of view of number theory, fills a gap in the l-adic cohomology information, which occurs exactly where there are 'equal characteristic primes'. Traditionally the preserve of ramification theory, crystalline cohomology converts this situation into Dieudonné module
theory, giving an important handle on arithmetic problems. Conjectures with wide scope on making this into formal statements were enunciated by Jean-Marc Fontaine, the resolution of which is called p-adic Hodge theory
.
for X a smooth complex variety. These groups are the cohomology of the complex of smooth differential form
s on X (with complex number coefficients), as these form a resolution of the constant sheaf C.
The algebraic de Rham cohomology is defined to be the hypercohomology of the complex of algebraic forms (Kähler differential
s) on X. The smooth i-forms form an acyclic sheaf, so the hypercohomology of the complex of smooth forms is the same as its cohomology, and the same is true for algebraic sheaves of i-forms over affine varieties, but algebraic sheaves of i-forms over non-affine varieties can have non-vanishing higher cohomology groups, so the hypercohomology can differ from the cohomology of the complex.
For smooth complex varieties Grothendieck (1963) showed that the algebraic de Rham cohomology is isomorphic to the usual smooth de Rham cohomology
and therefore (by de Rham's theorem) to the cohomology with complex coefficients. This definition of algebraic de Rham cohomology is available for algebraic varieties over any field k.
The classic reason (due to Serre) is that if X is a supersingular elliptic curve, then its ring of endomorphisms generates a quaternion algebra
over Q that is non-split at p and infinity. If X has a cohomology group over the p-adic integers with the expected dimension 2, the ring of endomorphisms would have a 2-dimensional representation; and this is not possible as it is non-split at p. (A quite subtle point is that if X is a supersingular elliptic curve over the prime field, with p elements, then its crystalline cohomology is a free rank 2 module over the p-adic integers. The argument given does not apply in this case, because some of the endomorphisms of supersingular elliptic curves are only defined over a quadratic extension of the field of order p.)
Grothendieck's crystalline cohomology theory gets around this obstruction because it takes values in the ring of Witt vector
s over the ground field
. So if the ground field is the algebraic closure
of the field of order p, its values are modules over the p-adic completion of the maximal unramified extension of the p-adic integers, a much larger ring containing n-th roots of unity for all n not divisible by p, rather than over the p-adic integers.
The idea of crystalline cohomology in characteristic 0 is to find a direct definition of a cohomology theory as the cohomology of constant sheaves on a suitable site
over X, called the infinitesimal site and then show it is the same as the de Rham cohomology of any lift.
The site Inf(X) is a category whose objects can be thought of as some sort of generalization of the conventional open sets of X. In characteristic 0 its objects are infinitesimal thickenings U→T of Zariski open subsets U of X. This means that U is the closed subscheme of a scheme T defined by a nilpotent sheaf of ideals on T; for example, Spec(k)→ Spec(k[x]/(x2)).
Grothendieck showed that for smooth schemes X over C, the cohomology of the sheaf OX on Inf(X) is the same as the usual (smooth or algebraic) de Rham cohomology.
giving the needed divided powers.
We will work over the ring Wn = W/pnW of Witt vectors of length n over a perfect field k of characteristic p>0. For example, k could be the finite field of order p, and Wn is then the ring Z/pnZ. (More generally one can work over a base scheme S which has a fixed sheaf of ideals I with a divided power structure.) If X is a scheme over k, then the crystalline site of X relative to Wn, denoted Cris(X/Wn), has as its objects pairs
U→T consisting of a closed immersion of a Zariski open subset U of X into some Wn-scheme T
defined by a sheaf of ideals J, together with a divided power structure on J compatible with the one on Wn.
Crystalline cohomology of a scheme X over k is defined to be the inverse limit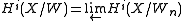
where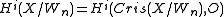
is the cohomology of the crystalline site of X/Wn with values in the sheaf of rings O = OX/Wn.
A key point of the theory is that the crystalline cohomology of a smooth scheme X over k can often be calculated in terms of the algebraic de Rham cohomology of a proper and smooth lifting of X to a scheme Z over W. There is a canonical isomorphism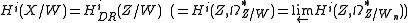
of the crystalline cohomology of X with the de Rham cohomology of Z over the formal scheme
of W
(an inverse limit of the hypercohomology of the complexes of differential forms).
Conversely the de Rham cohomology of X can be recovered as the reduction mod p of its crystalline cohomology (after taking higher Tors into account).
OX/S(T) = coordinate ring of T, where we write T as an abbreviation for
an object U→T of Cris(X/S).
A crystal on the site Cris(X/S) is a sheaf F of OX/S modules that is rigid in the following sense:
This is similar to the definition of a quasicoherent sheaf of modules in the Zariski topology.
An example of a crystal is the sheaf OX/S.
The term crystal attached to the theory, explained in Grothendieck's letter to Tate
(1966), was a metaphor inspired by certain properties of algebraic differential equation
s. These had played a role in p-adic cohomology theories (precursors of the crystalline theory, introduced in various forms by Dwork
, Monsky
, Washnitzer, Lubkin and Katz
) particularly in Dwork's work. Such differential equations can be formulated easily enough by means of the algebraic Koszul connections, but in the p-adic theory the analogue of analytic continuation
is more mysterious (since p-adic discs tend to be disjoint rather than overlap). By decree, a crystal would have the 'rigidity' and the 'propagation' notable in the case of the analytic continuation of complex analytic functions. (Cf. also the rigid analytic space
s introduced by Tate
, in the 1960s, when these matters were actively being debated.)
Weil cohomology theory
In algebraic geometry, a Weil cohomology or Weil cohomology theory is a cohomology satisfying certain axioms concerning the interplay of algebraic cycles and cohomology groups. The name is in honor of André Weil...
for schemes introduced by and developed by . Its values are modules over rings of Witt vector
Witt vector
In mathematics, a Witt vector is an infinite sequence of elements of a commutative ring. Ernst Witt showed how to put a ring structure on the set of Witt vectors, in such a way that the ring of Witt vectors over the finite field of order p is the ring of p-adic integers.-Motivation:Any p-adic...
s over the base field.
Crystalline cohomology is partly inspired by the p-adic proof in of part of the Weil conjectures
Weil conjectures
In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
and is closely related to the (algebraic) de Rham cohomology introduced by Grothendieck (1963). Roughly speaking, crystalline cohomology of a variety X in characteristic p is the de Rham cohomology of a smooth lift of X to characteristic 0, while de Rham cohomology of X is the crystalline cohomology reduced mod p (after taking into account higher Tors).
The idea of crystalline cohomology, roughly, is to replace the Zariski open sets of a scheme by infinitesimal thickenings of Zariski open sets with divided power structure
Divided power structure
In mathematics, specifically commutative algebra, a divided power structure is a way of making expressions of the form x^n / n! meaningful even when it is not possible to actually divide by n!.- Definition :Let A be a commutative ring with an ideal I...
s. The motivation for this is that it can then be calculated by taking a local lifting of a scheme from characteristic p to characteristic 0 and employing an appropriate version of algebraic de Rham cohomology.
Crystalline cohomology only works well for smooth proper schemes. Rigid cohomology
Rigid cohomology
In mathematics, rigid cohomology is a p-adic cohomology theory introduced by . It extends crystalline cohomology to schemes that need not be proper or smooth, and extends Monsky–Washnitzer cohomology to non-affine varieties....
extends it to more general schemes.
Applications
For schemes in characteristic p, crystalline cohomology theory can handle questions about p-torsion in cohomology groups better than p-adic étale cohomology. This makes it a natural backdrop for much of the work on p-adic L-functionP-adic L-function
In mathematics, a p-adic zeta function, or more generally a p-adic L-function, is a function analogous to the Riemann zeta function, or more general L-functions, but whose domain and target are p-adic...
s.
Crystalline cohomology, from the point of view of number theory, fills a gap in the l-adic cohomology information, which occurs exactly where there are 'equal characteristic primes'. Traditionally the preserve of ramification theory, crystalline cohomology converts this situation into Dieudonné module
Dieudonné module
In mathematics, a Dieudonné module introduced by , is a module over the non-commutative Dieudonné ring, which is generated over the ring of Witt vectors by two special endomorphisms F and V called the Frobenius and Verschiebung operators...
theory, giving an important handle on arithmetic problems. Conjectures with wide scope on making this into formal statements were enunciated by Jean-Marc Fontaine, the resolution of which is called p-adic Hodge theory
P-adic Hodge theory
In mathematics, p-adic Hodge theory is a theory that provides a way to classify and study p-adic Galois representations of characteristic 0 local fields with residual characteristic p . The theory has its beginnings in Jean-Pierre Serre and John Tate's study of Tate modules of abelian varieties and...
.
de Rham cohomology
De Rham cohomology solves the problem of finding an algebraic definition of the cohomology groups (singular cohomology)- Hi(X,C)
for X a smooth complex variety. These groups are the cohomology of the complex of smooth differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on X (with complex number coefficients), as these form a resolution of the constant sheaf C.
The algebraic de Rham cohomology is defined to be the hypercohomology of the complex of algebraic forms (Kähler differential
Kähler differential
In mathematics, Kähler differentials provide an adaptation of differential forms to arbitrary commutative rings or schemes.-Presentation:The idea was introduced by Erich Kähler in the 1930s...
s) on X. The smooth i-forms form an acyclic sheaf, so the hypercohomology of the complex of smooth forms is the same as its cohomology, and the same is true for algebraic sheaves of i-forms over affine varieties, but algebraic sheaves of i-forms over non-affine varieties can have non-vanishing higher cohomology groups, so the hypercohomology can differ from the cohomology of the complex.
For smooth complex varieties Grothendieck (1963) showed that the algebraic de Rham cohomology is isomorphic to the usual smooth de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
and therefore (by de Rham's theorem) to the cohomology with complex coefficients. This definition of algebraic de Rham cohomology is available for algebraic varieties over any field k.
Coefficients
If X is a variety over an algebraically closed field of characteristic p > 0, then the l-adic cohomology groups for l any prime number other than p give satisfactory cohomology groups of X, with coefficients in the ring Zl of l-adic integers. It is not possible in general to find similar cohomology groups with coefficients in the p-adic numbers (or the rationals, or the integers).The classic reason (due to Serre) is that if X is a supersingular elliptic curve, then its ring of endomorphisms generates a quaternion algebra
Quaternion algebra
In mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars , i.e...
over Q that is non-split at p and infinity. If X has a cohomology group over the p-adic integers with the expected dimension 2, the ring of endomorphisms would have a 2-dimensional representation; and this is not possible as it is non-split at p. (A quite subtle point is that if X is a supersingular elliptic curve over the prime field, with p elements, then its crystalline cohomology is a free rank 2 module over the p-adic integers. The argument given does not apply in this case, because some of the endomorphisms of supersingular elliptic curves are only defined over a quadratic extension of the field of order p.)
Grothendieck's crystalline cohomology theory gets around this obstruction because it takes values in the ring of Witt vector
Witt vector
In mathematics, a Witt vector is an infinite sequence of elements of a commutative ring. Ernst Witt showed how to put a ring structure on the set of Witt vectors, in such a way that the ring of Witt vectors over the finite field of order p is the ring of p-adic integers.-Motivation:Any p-adic...
s over the ground field
Ground field
In mathematics, a ground field is a field K fixed at the beginning of the discussion. It is used in various areas of algebra: for example in linear algebra where the concept of a vector space may be developed over any field; and in algebraic geometry, where in the foundational developments of André...
. So if the ground field is the algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of the field of order p, its values are modules over the p-adic completion of the maximal unramified extension of the p-adic integers, a much larger ring containing n-th roots of unity for all n not divisible by p, rather than over the p-adic integers.
Motivation
One idea for defining a Weil cohomology theory of a variety X over a field k of characteristic p is to 'lift' it to a variety X* over the ring of Witt vectors of k (that gives back X on reduction mod p), then take the de Rham cohomology of this lift. The problem is that it is not at all obvious that this cohomology is independent of the choice of lifting.The idea of crystalline cohomology in characteristic 0 is to find a direct definition of a cohomology theory as the cohomology of constant sheaves on a suitable site
- Inf(X)
over X, called the infinitesimal site and then show it is the same as the de Rham cohomology of any lift.
The site Inf(X) is a category whose objects can be thought of as some sort of generalization of the conventional open sets of X. In characteristic 0 its objects are infinitesimal thickenings U→T of Zariski open subsets U of X. This means that U is the closed subscheme of a scheme T defined by a nilpotent sheaf of ideals on T; for example, Spec(k)→ Spec(k[x]/(x2)).
Grothendieck showed that for smooth schemes X over C, the cohomology of the sheaf OX on Inf(X) is the same as the usual (smooth or algebraic) de Rham cohomology.
Crystalline cohomology
In characteristic p the most obvious analogue of the crystalline site defined above in characteristic 0 does not work. The reason is roughly that in order to prove exactness of the de Rham complex, one needs some sort of Poincaré lemma, whose proof in turn uses integration, and integration requires various divided powers, which exist in characteristic 0 but not always in characteristic p. Grothendieck solved this problem by defining objects of the crystalline site of X to be roughly infinitesimal thickenings of Zariski open subsets of X, together with a divided power structureDivided power structure
In mathematics, specifically commutative algebra, a divided power structure is a way of making expressions of the form x^n / n! meaningful even when it is not possible to actually divide by n!.- Definition :Let A be a commutative ring with an ideal I...
giving the needed divided powers.
We will work over the ring Wn = W/pnW of Witt vectors of length n over a perfect field k of characteristic p>0. For example, k could be the finite field of order p, and Wn is then the ring Z/pnZ. (More generally one can work over a base scheme S which has a fixed sheaf of ideals I with a divided power structure.) If X is a scheme over k, then the crystalline site of X relative to Wn, denoted Cris(X/Wn), has as its objects pairs
U→T consisting of a closed immersion of a Zariski open subset U of X into some Wn-scheme T
defined by a sheaf of ideals J, together with a divided power structure on J compatible with the one on Wn.
Crystalline cohomology of a scheme X over k is defined to be the inverse limit
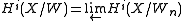
where
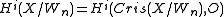
is the cohomology of the crystalline site of X/Wn with values in the sheaf of rings O = OX/Wn.
A key point of the theory is that the crystalline cohomology of a smooth scheme X over k can often be calculated in terms of the algebraic de Rham cohomology of a proper and smooth lifting of X to a scheme Z over W. There is a canonical isomorphism
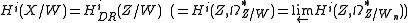
of the crystalline cohomology of X with the de Rham cohomology of Z over the formal scheme
Formal scheme
In mathematics, specifically in algebraic geometry, a formal scheme is a type of space which includes data about its surroundings. Unlike an ordinary scheme, a formal scheme includes infinitesimal data that, in effect, points in a direction off of the scheme...
of W
(an inverse limit of the hypercohomology of the complexes of differential forms).
Conversely the de Rham cohomology of X can be recovered as the reduction mod p of its crystalline cohomology (after taking higher Tors into account).
Crystals
If X is a scheme over S then the sheaf OX/S is defined byOX/S(T) = coordinate ring of T, where we write T as an abbreviation for
an object U→T of Cris(X/S).
A crystal on the site Cris(X/S) is a sheaf F of OX/S modules that is rigid in the following sense:
- for any map f between objects T, T′ of Cris(X/S), the natural map from f*F(T) to F(T′) is an isomorphism.
This is similar to the definition of a quasicoherent sheaf of modules in the Zariski topology.
An example of a crystal is the sheaf OX/S.
The term crystal attached to the theory, explained in Grothendieck's letter to Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
(1966), was a metaphor inspired by certain properties of algebraic differential equation
Algebraic differential equation
In mathematics, an algebraic differential equation is a differential equation that can be expressed by means of differential algebra. There are several such notions, according to the concept of differential algebra used....
s. These had played a role in p-adic cohomology theories (precursors of the crystalline theory, introduced in various forms by Dwork
Bernard Dwork
Bernard Morris Dwork was an American mathematician, known for his application of p-adic analysis to local zeta functions, and in particular for the first general results on the Weil conjectures. Together with Kenkichi Iwasawa he received the Cole Prize in 1962.Dwork received his Ph.D. at Columbia...
, Monsky
Paul Monsky
Paul Monsky is an American mathematician and professor at Brandeis University.After earning a Bachelors degree from Swarthmore College, he received his Ph. D. in 1962 from the University of Chicago under the supervision of Walter Bailey...
, Washnitzer, Lubkin and Katz
Nick Katz
Nicholas Michael Katz is an American mathematician, working in the fields of algebraic geometry, particularly on p-adic methods, monodromy and moduli problems, and number theory...
) particularly in Dwork's work. Such differential equations can be formulated easily enough by means of the algebraic Koszul connections, but in the p-adic theory the analogue of analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
is more mysterious (since p-adic discs tend to be disjoint rather than overlap). By decree, a crystal would have the 'rigidity' and the 'propagation' notable in the case of the analytic continuation of complex analytic functions. (Cf. also the rigid analytic space
Rigid analytic space
In mathematics, a rigid analytic space is an analogue of a complex analytic space over a nonarchimedean field. They were introduced by John Tate in 1962, as an outgrowth of his work on uniformizing p-adic elliptic curves with bad reduction using the multiplicative group...
s introduced by Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
, in the 1960s, when these matters were actively being debated.)

