
Supersingular elliptic curve
Encyclopedia
In algebraic geometry
, a branch of mathematics
, supersingular elliptic curves form a certain class of elliptic curve
s over a field of characteristic p > 0. Elliptic curves over such fields which are not supersingular are called ordinary and these two classes of elliptic curves behave fundamentally differently in many aspects.
 and E an elliptic curve
and E an elliptic curve
over K. Then the -valued points
-valued points 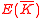 have the structure of an abelian group. For every n, we have a multiplication map
have the structure of an abelian group. For every n, we have a multiplication map 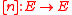 . Its kernel is denoted by
. Its kernel is denoted by 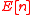 . Now assume that the characteristic of K is p > 0. Then one can show that either
. Now assume that the characteristic of K is p > 0. Then one can show that either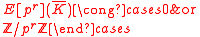
for r = 1, 2, 3, ... In the first case, E is called supersingular. Otherwise it is called ordinary. The term 'supersingular' does not mean, of course, that E is singular since all elliptic curves are smooth.
 .
.
The elliptic curve E is supersingular if and only if equals 0.
equals 0.
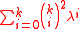
vanishes, where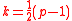 . Using this formula, one can show that there are only finitely many supersingular elliptic curves for every K.
. Using this formula, one can show that there are only finitely many supersingular elliptic curves for every K.

is supersingular (see Washington2003, p. 122).

is supersingular (see Washington2003, p. 122).
showed that any elliptic curve defined over the rationals is supersingular for an infinite number of primes. give a table of all supersingular curves for primes up to 307. For the first few primes the supersingular elliptic curves are given as follows. The number of supersingular values of j other than 0 or 1728 is the integer part of (p−1)/12.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, supersingular elliptic curves form a certain class of elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s over a field of characteristic p > 0. Elliptic curves over such fields which are not supersingular are called ordinary and these two classes of elliptic curves behave fundamentally differently in many aspects.
Definition
Let K be a field with algebraic closure and E an elliptic curve
and E an elliptic curveElliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
over K. Then the
 -valued points
-valued points 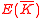 have the structure of an abelian group. For every n, we have a multiplication map
have the structure of an abelian group. For every n, we have a multiplication map 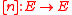 . Its kernel is denoted by
. Its kernel is denoted by 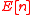 . Now assume that the characteristic of K is p > 0. Then one can show that either
. Now assume that the characteristic of K is p > 0. Then one can show that either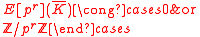
for r = 1, 2, 3, ... In the first case, E is called supersingular. Otherwise it is called ordinary. The term 'supersingular' does not mean, of course, that E is singular since all elliptic curves are smooth.
Equivalent conditions
There is a number of equivalent conditions to supersingularity:- Supersingular elliptic curves have many endomorphisms in the sense that an elliptic curve is supersingular if and only if its endomorphism algebra (over
 ) is an order in a quaternion algebraQuaternion algebraIn mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars , i.e...
) is an order in a quaternion algebraQuaternion algebraIn mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars , i.e...
. Thus, their endomorphism group has rank 4, while the endomorphism group of every other elliptic curve has only rank 1 or 2.
- Let G be the formal groupFormal groupIn mathematics, a formal group law is a formal power series behaving as if it were the product of a Lie group. They were introduced by . The term formal group sometimes means the same as formal group law, and sometimes means one of several generalizations. Formal groups are intermediate between...
associated to E. Since K is of positive characteristic, we can define its height ht(G), which is 2 if and only if E is supersingular and else is 1.
- We have a Frobenius morphism
 , which induces a map in cohomology
, which induces a map in cohomology
 .
.The elliptic curve E is supersingular if and only if
 equals 0.
equals 0.- Suppose E is in Legendre form, defined by the equation
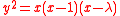 . Then E is supersingular if and only if the sum
. Then E is supersingular if and only if the sum
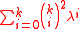
vanishes, where
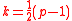 . Using this formula, one can show that there are only finitely many supersingular elliptic curves for every K.
. Using this formula, one can show that there are only finitely many supersingular elliptic curves for every K.Examples
- If K is a field of characteristic 2, every elliptic curve defined by an equation of the form

is supersingular (see Washington2003, p. 122).
- If K is a field of characteristic 3, every elliptic curve defined by an equation of the form

is supersingular (see Washington2003, p. 122).
- For
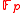 with p>3 we have that the elliptic curve defined by
with p>3 we have that the elliptic curve defined by 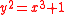 is supersingular if and only if
is supersingular if and only if  and the elliptic curve defined by
and the elliptic curve defined by 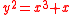 is supersingular if and only if
is supersingular if and only if  (see Washington2003, 4.35).
(see Washington2003, 4.35).
- There are also more exotic examples: The elliptic curve given by
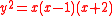 is nonsingular over
is nonsingular over  for
for 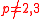 . It is supersingular for p = 23 and ordinary for every other
. It is supersingular for p = 23 and ordinary for every other  (see Hartshorne1977, 4.23.6).
(see Hartshorne1977, 4.23.6).
showed that any elliptic curve defined over the rationals is supersingular for an infinite number of primes. give a table of all supersingular curves for primes up to 307. For the first few primes the supersingular elliptic curves are given as follows. The number of supersingular values of j other than 0 or 1728 is the integer part of (p−1)/12.
| prime | supersingular j invariants |
|---|---|
| 2 | 0 |
| 3 | 0=1728 |
| 5 | 0 |
| 7 | 6=1728 |
| 11 | 0, 1=1728 |
| 13 | 5 |
| 17 | 0,8 |
| 19 | 7, 1728 |
| 23 | 0,19, 1728 |
| 29 | 0,2, 25 |
| 31 | 2, 4, 1728 |
| 37 | 8, 3±√15 |

