
P-adic L-function
Encyclopedia
In mathematics
, a p-adic zeta function, or more generally a p-adic L-function, is a function analogous to the Riemann zeta function, or more general L-functions
, but whose domain and target
are p-adic (where p is a prime number
). For example, the domain could be the p-adic integers Zp, a profinite p-group, or a p-adic family of Galois representations, and the image could be the p-adic numbers
Qp or its algebraic closure
.
The source of a p-adic L-function tends to be one of two types. The first source—from which Tomio Kubota
and Heinrich-Wolfgang Leopoldt
gave the first construction of a p-adic L-function —is via the p-adic interpolation of special values of L-functions
. For example, Kubota–Leopoldt used Kummer's congruence
s for Bernoulli number
s to construct a p-adic L-function, the p-adic Riemann zeta function ζp(s), whose values at negative odd integers are those of the Riemann zeta function at negative odd integers (up to an explicit correction factor). p-adic L-functions arising in this fashion are typically referred to as analytic p-adic L-functions. The other major source of p-adic L-functions—first discovered by Kenkichi Iwasawa
—is from the arithmetic of cyclotomic field
s, or more generally, certain Galois module
s over towers of cyclotomic fields or even more general towers. A p-adic L-function arising in this way is typically called an arithmetic p-adic L-function as it encodes arithmetic data of the Galois module involved. The main conjecture of Iwasawa theory (now a theorem due to Barry Mazur
and Andrew Wiles
) is the statement that the Kubota–Leopoldt p-adic L-function and an arithmetic analogue constructed by Iwasawa theory are essentially the same. In more general situations where both analytic and arithmetic p-adic L-functions are constructed (or expected), the statement that they agree is called the main conjecture of Iwasawa theory for that situation. Such conjectures represent formal statements concerning the philosophy that special values of L-functions contain arithmetic information.

The Dirichlet L-function at negative integers is given by
where Bn,χ is a generalized Bernoulli number defined by
for χ a Dirichlet character with conductor f.
More precisely, Lp(s,χ) is the unique continuous function of the p-adic number s such that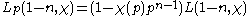
for positive integers n divisible by p−1. The right hand side is just the usual Dirichlet L-function, except that the Euler factor at p is removed, otherwise it would not be p-adically continuous. The continuity of the right hand side is closely related to the Kummer congruences.
When n is not divisible by p−1 this does not usually hold; instead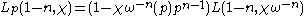
for positive integers n.
Here χ is twisted by a power of the Teichmuller character
ω.
) on p-profinite Galois groups. The translation between this point of view and the original point of view of Kubota–Leopoldt (as Qp-valued functions on Zp) is via the Mazur–Mellin transform (and class field theory
).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a p-adic zeta function, or more generally a p-adic L-function, is a function analogous to the Riemann zeta function, or more general L-functions
L-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
, but whose domain and target
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
are p-adic (where p is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
). For example, the domain could be the p-adic integers Zp, a profinite p-group, or a p-adic family of Galois representations, and the image could be the p-adic numbers
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
Qp or its algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
.
The source of a p-adic L-function tends to be one of two types. The first source—from which Tomio Kubota
Tomio Kubota
is a Japanese mathematician, who studies number theory. His contributions include works on p-adic L functions and real-analytic automorphic forms.His work on p-adic L-functions, later recognised as an aspect of Iwasawa theory, was jointly with Leopoldt....
and Heinrich-Wolfgang Leopoldt
Heinrich-Wolfgang Leopoldt
Heinrich-Wolfgang Leopoldt was a German mathematician, who worked on algebraic number theory.Leopoldt earned his PhD in 1954 at the University of Hamburg under Helmut Hasse with the thesis Über Einheitengruppe und Klassenzahl reeller algebraischer Zahlkörper...
gave the first construction of a p-adic L-function —is via the p-adic interpolation of special values of L-functions
Special values of L-functions
In mathematics, the study of special values of L-functions is a subfield of number theory devoted to generalising formulae such as the Leibniz formula for pi, namely...
. For example, Kubota–Leopoldt used Kummer's congruence
Kummer's congruence
In mathematics, Kummer's congruences are some congruences involving Bernoulli numbers, found by . used Kummer's congruences to define the p-adic zeta function.-Statement:...
s for Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s to construct a p-adic L-function, the p-adic Riemann zeta function ζp(s), whose values at negative odd integers are those of the Riemann zeta function at negative odd integers (up to an explicit correction factor). p-adic L-functions arising in this fashion are typically referred to as analytic p-adic L-functions. The other major source of p-adic L-functions—first discovered by Kenkichi Iwasawa
Kenkichi Iwasawa
Kenkichi Iwasawa was a Japanese mathematician who is known for his influence on algebraic number theory.Iwasawa was born in Shinshuku-mura, a town near Kiryū, in Gunma Prefecture...
—is from the arithmetic of cyclotomic field
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
s, or more generally, certain Galois module
Galois module
In mathematics, a Galois module is a G-module where G is the Galois group of some extension of fields. The term Galois representation is frequently used when the G-module is a vector space over a field or a free module over a ring, but can also be used as a synonym for G-module...
s over towers of cyclotomic fields or even more general towers. A p-adic L-function arising in this way is typically called an arithmetic p-adic L-function as it encodes arithmetic data of the Galois module involved. The main conjecture of Iwasawa theory (now a theorem due to Barry Mazur
Barry Mazur
-Life:Born in New York City, Mazur attended the Bronx High School of Science and MIT, although he did not graduate from the latter on account of failing a then-present ROTC requirement. Regardless, he was accepted for graduate school and received his Ph.D. from Princeton University in 1959,...
and Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
) is the statement that the Kubota–Leopoldt p-adic L-function and an arithmetic analogue constructed by Iwasawa theory are essentially the same. In more general situations where both analytic and arithmetic p-adic L-functions are constructed (or expected), the statement that they agree is called the main conjecture of Iwasawa theory for that situation. Such conjectures represent formal statements concerning the philosophy that special values of L-functions contain arithmetic information.
Dirichlet L-functions
The Dirichlet L-function is given by the analytic continuation of
The Dirichlet L-function at negative integers is given by

where Bn,χ is a generalized Bernoulli number defined by

for χ a Dirichlet character with conductor f.
Definition using interpolation
The Kubota–Leopoldt p-adic L-function Lp(s, χ) interpolates the Dirichlet L-function with the Euler factor at p removed.More precisely, Lp(s,χ) is the unique continuous function of the p-adic number s such that
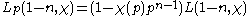
for positive integers n divisible by p−1. The right hand side is just the usual Dirichlet L-function, except that the Euler factor at p is removed, otherwise it would not be p-adically continuous. The continuity of the right hand side is closely related to the Kummer congruences.
When n is not divisible by p−1 this does not usually hold; instead
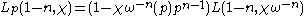
for positive integers n.
Here χ is twisted by a power of the Teichmuller character
Teichmüller character
In number theory, the Teichmüller character ω is a character of ×, where q = p or 4 if p odd or even, taking values in the roots of unity of the p-adic integers. It was introduced by Oswald Teichmüller...
ω.
Viewed as a p-adic measure
p-adic L-functions can also be thought of as p-adic measures (or p-adic distributionsP-adic distribution
In mathematics, a p-adic distribution is an analogue of ordinary distributions that takes values in a ring of p-adic numbers.-Definition:...
) on p-profinite Galois groups. The translation between this point of view and the original point of view of Kubota–Leopoldt (as Qp-valued functions on Zp) is via the Mazur–Mellin transform (and class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
).

