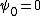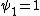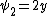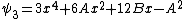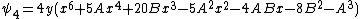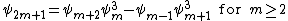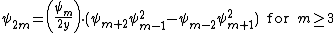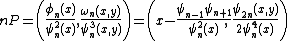Division polynomials
Encyclopedia
In mathematics
the division polynomials provide a way to calculate multiples of points on elliptic curves over Finite fields. They play a central role in the study of counting points on elliptic curves
in Schoof's algorithm
.
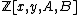with 
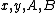free variables that is recursively defined by:
The polynomial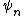
is called the nth division polynomial.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the division polynomials provide a way to calculate multiples of points on elliptic curves over Finite fields. They play a central role in the study of counting points on elliptic curves
Counting points on elliptic curves
An important aspect in the study of elliptic curves is devising effective ways of counting points on the curve. There have been several approaches to do so, and the algorithms devised have proved to be useful tools in the study of various fields such as number theory, and more recently in...
in Schoof's algorithm
Schoof's algorithm
Schoof's algorithm is an efficient algorithm to count points on elliptic curves over finite fields. The algorithm has applications in elliptic curve cryptography where it is important to know the number of points to judge the difficulty of solving the discrete logarithm problem in the group of...
.
Definition
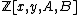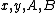The division polynomials are a sequence of polynomials in with free variables that is recursively defined by:
The polynomial
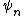is called the nth division polynomial.Properties
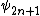is a polynomial in 
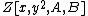, while 
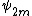is a polynomial in 
.- The division polynomials form an elliptic divisibility sequenceElliptic divisibility sequenceIn mathematics, an elliptic divisibility sequence is a sequence of integers satisfying a nonlinear recursion relation arising from division polynomials on elliptic curves. EDS were first defined, and their arithmetic properties studied, by Morgan Ward...
. Moreover all nonsingular elliptic divisibility sequences arise this way. - If an elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
is given in the Weierstrass form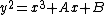 
over some field 
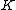, i.e. 
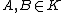one can evaluate the division polynomials at those 
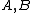and consider them as polynomials in the coordinate ring. Then the powers of 
can only be less or equal to 1, as 
is replaced by 
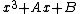. In particular, 
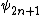is a univariate polynomial in 
only. The roots of the 
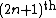division polynomial 
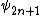are exactly the 
coordinates of the points of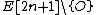 
, where 
is the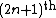 
torsion subgroupTorsion subgroupIn the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
of the group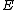
of an elliptic curve. - Given a point
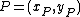on the elliptic curve 
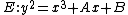over some field 
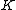, we can express the coordinates of the nth multiple of 
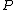in terms of division polynomials:
-
- where
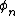and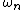 
are defined by: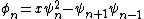 
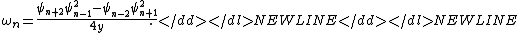
Using the relation between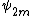
and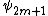 
, along with the equation of the curve, we have that 
, 
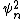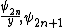and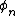 
are all functions in the variable 
.
Let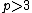
be prime and let 
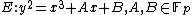be an elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
over the finite field
. The 
-torsion group of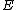 
over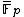 
is isomorphic to 
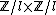if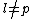 
and to 
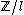of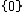 
otherwise which means that the degree of 
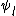is 
, 
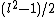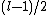or 0.
René Schoof observed that working modulo the
th division polynomial means working with all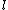 
-torsion points simultaneously. This is heavily used in Schoof's algorithmSchoof's algorithmSchoof's algorithm is an efficient algorithm to count points on elliptic curves over finite fields. The algorithm has applications in elliptic curve cryptography where it is important to know the number of points to judge the difficulty of solving the discrete logarithm problem in the group of...
for counting points on elliptic curves.
