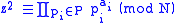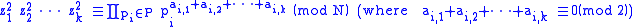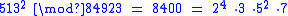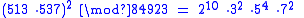Dixon's factorization method
Encyclopedia
In number theory
, Dixon's factorization method (also Dixon's random squares method or Dixon's algorithm) is a general-purpose integer factorization
algorithm
; it is the prototypical factor base
method, and the only factor base method for which a run-time bound not reliant on conjectures about the smoothness properties of values of a polynomial is known.
The algorithm was designed by John D. Dixon, a mathematician at Carleton University
, and was published in 1981.
modulo the integer N which we intend to factor. Fermat's factorization algorithm finds such a congruence by selecting random or pseudo-random x values and hoping that the integer x2 mod N is a perfect square (in the integers):
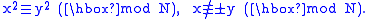
For example, if , we notice (by starting at 292, the first number greater than and counting up) that is 256, the square of 16. So . Computing the greatest common divisor
of and N using Euclid's algorithm gives us 163, which is a factor of N.
In practice, selecting random x values will take an impractically long time to find a congruence of squares, since there are only squares less than N.
Dixon's method replaces the condition "is the square of an integer" with the much weaker one "has only small prime factors"; for example, there are 292 squares less than 84923; 662 numbers less than 84923 whose prime factors are only 2,3,5 or 7; and 4767 whose prime factors are all less than 30. (Such numbers are called B-smooth
with respect to some bound B.)
If we have lots of numbers
whose squares can be factorized as 
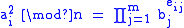for a fixed set 
of small primes, linear algebra modulo 2 on the matrix 
will give us a subset of the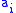 
whose squares combine to a product of small primes to an even power — that is, a subset of the 
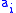whose squares multiply to the square of a (hopefully different) number mod N.
(which we will call P), the set of all primes less than or equal to B. Next, we search for positive integers z such that z2 mod N is B-smooth. We can therefore write, for suitable exponents ak,
When we have generated enough of these relations (it's generally sufficient that the number of relations be a few more than the size of P), we can use the methods of linear algebra
(for example, Gaussian elimination
) to multiply together these various relations in such a way that the exponents of the primes on the right-hand side are all even:
This gives us a congruence of squares
of the form which can be turned into a factorization of N, This factorization might turn out to be trivial (i.e. ), which can only happen if in which case we have to try again with a different combination of relations; but with luck we will get a nontrivial pair of factors of N, and the algorithm will terminate.
is then P = {2, 3, 5, 7}. We then search randomly for integers between
and N whose squares are B-smooth
. Suppose that two of the numbers we find are 513 and 537:
So
Then
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Dixon's factorization method (also Dixon's random squares method or Dixon's algorithm) is a general-purpose integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
; it is the prototypical factor base
Factor base
In computational number theory, the factor base is a mathematical tool commonly used in algorithms involving extensive sieving of potential factors.-Usage:...
method, and the only factor base method for which a run-time bound not reliant on conjectures about the smoothness properties of values of a polynomial is known.
The algorithm was designed by John D. Dixon, a mathematician at Carleton University
Carleton University
Carleton University is a comprehensive university located in the capital of Canada, Ottawa, Ontario. The enabling legislation is The Carleton University Act, 1952, S.O. 1952. Founded as a small college in 1942, Carleton now offers over 65 programs in a diverse range of disciplines. Carleton has...
, and was published in 1981.
Basic idea
Dixon's method is based on finding a congruence of squaresCongruence of squares
In number theory, a congruence of squares is a congruence commonly used in integer factorization algorithms.-Derivation:Given a positive integer n, Fermat's factorization method relies on finding numbers x, y satisfying the equality...
modulo the integer N which we intend to factor. Fermat's factorization algorithm finds such a congruence by selecting random or pseudo-random x values and hoping that the integer x2 mod N is a perfect square (in the integers):
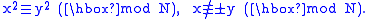
For example, if , we notice (by starting at 292, the first number greater than and counting up) that is 256, the square of 16. So . Computing the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of and N using Euclid's algorithm gives us 163, which is a factor of N.
In practice, selecting random x values will take an impractically long time to find a congruence of squares, since there are only squares less than N.
Dixon's method replaces the condition "is the square of an integer" with the much weaker one "has only small prime factors"; for example, there are 292 squares less than 84923; 662 numbers less than 84923 whose prime factors are only 2,3,5 or 7; and 4767 whose prime factors are all less than 30. (Such numbers are called B-smooth
Smooth number
In number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:...
with respect to some bound B.)
If we have lots of numbers
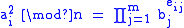whose squares can be factorized as for a fixed set of small primes, linear algebra modulo 2 on the matrix will give us a subset of the 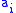whose squares combine to a product of small primes to an even power — that is, a subset of the 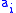whose squares multiply to the square of a (hopefully different) number mod N.Method
Suppose we are trying to factor the composite number N. We choose a bound B, and identify the factor baseFactor base
In computational number theory, the factor base is a mathematical tool commonly used in algorithms involving extensive sieving of potential factors.-Usage:...
(which we will call P), the set of all primes less than or equal to B. Next, we search for positive integers z such that z2 mod N is B-smooth. We can therefore write, for suitable exponents ak,
When we have generated enough of these relations (it's generally sufficient that the number of relations be a few more than the size of P), we can use the methods of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
(for example, Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
) to multiply together these various relations in such a way that the exponents of the primes on the right-hand side are all even:
This gives us a congruence of squares
Congruence of squares
In number theory, a congruence of squares is a congruence commonly used in integer factorization algorithms.-Derivation:Given a positive integer n, Fermat's factorization method relies on finding numbers x, y satisfying the equality...
of the form which can be turned into a factorization of N, This factorization might turn out to be trivial (i.e. ), which can only happen if in which case we have to try again with a different combination of relations; but with luck we will get a nontrivial pair of factors of N, and the algorithm will terminate.
Example
We will try to factor N = 84923 using bound B = 7. Our factor baseFactor base
In computational number theory, the factor base is a mathematical tool commonly used in algorithms involving extensive sieving of potential factors.-Usage:...
is then P = {2, 3, 5, 7}. We then search randomly for integers between
and N whose squares are B-smoothSmooth number
In number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:...
. Suppose that two of the numbers we find are 513 and 537:
So
Then
-
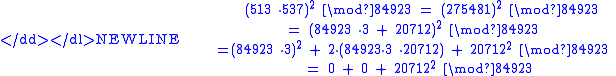
That is,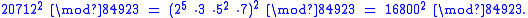
The resulting factorization is 84923 = gcd(20712 − 16800, 84923) × gcd(20712 + 16800, 84923) = 163 × 521.
Optimizations
The quadratic sieveQuadratic sieveThe quadratic sieve algorithm is a modern integer factorization algorithm and, in practice, the second fastest method known . It is still the fastest for integers under 100 decimal digits or so, and is considerably simpler than the number field sieve...
is an optimization of Dixon's method. It selects values of x close to the square root of N such that x2 modulo N is small, thereby largely increasing the chance of obtaining a smooth number.
Other ways to optimize Dixon's method include using a better algorithm to solve the matrix equation, taking advantage of the sparsity of the matrix: a number z cannot have more than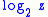
factors, so each row of the matrix is almost all zeros. In practice, the block Lanczos algorithmBlock Lanczos algorithm for nullspace of a matrix over a finite fieldThe block Lanczos algorithm for nullspace of a matrix over a finite field is a procedure for finding the nullspace of a matrix using only multiplication of the matrix by long, thin matrices...
is often used. Also, the size of the factor base must be chosen carefully: if it is too small, it will be difficult to find numbers that factorize completely over it, and if it is too large, more relations will have to be collected.
A more sophisticated analysis, using the approximation that a number has all its prime factors less than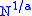
with probability about 
(an approximation to the Dickman–de Bruijn function), indicates that choosing too small a factor base is much worse than too large, and that the ideal factor base size is some power of 
.
The optimal complexity of Dixon's method is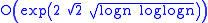
in big-O notation, or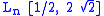
in L-notationL-notationL-notation is an asymptotic notation analogous to big-O notation, denoted as L_n[\alpha,c] for a bound variable n tending to infinity. Like big-O notation, it is usually used to roughly convey the computational complexity of a particular algorithm....
.