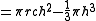Dome (mathematics)
Encyclopedia
In mathematics
, a dome is a closed geometrical
surface
which can be obtained by sectioning off a portion of a sphere
with an intersecting plane
. It consists of two parts: (1) a flat disk
, which is joined to (2) a convex surface whose curvature
is uniform and which has a circular boundary: this boundary joins with the rim of the disk. The disk can be referred to as the dome's "base".
A pair of parameters are enough to describe a dome: (1) its diameter
and (2) its height
. The diameter refers to the size of the base, whereas the height refers to the perpendicular distance between the center of the base and the center of the concavity.
The dome's convex region, which may be referred to here as "ceiling" (in an analogy with architecture) has a radius of curvature
rc given by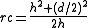
where d is the diameter and h is the height.
The kind of dome described so far is a spherical dome, though there are variants, such as the spheroidal dome, obtained by sectioning off a portion of a spheroid
so that the resulting dome is symmetrical (having an axis of rotation), and likewise the ellipsoidal dome derived from the ellipsoid.
The surface area of a spherical dome's ceiling is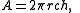
and the dome's volume is given by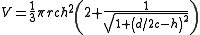
where r=d/2.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a dome is a closed geometrical
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
which can be obtained by sectioning off a portion of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
with an intersecting plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
. It consists of two parts: (1) a flat disk
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
, which is joined to (2) a convex surface whose curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
is uniform and which has a circular boundary: this boundary joins with the rim of the disk. The disk can be referred to as the dome's "base".
A pair of parameters are enough to describe a dome: (1) its diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
and (2) its height
Height
Height is the measurement of vertical distance, but has two meanings in common use. It can either indicate how "tall" something is, or how "high up" it is. For example "The height of the building is 50 m" or "The height of the airplane is 10,000 m"...
. The diameter refers to the size of the base, whereas the height refers to the perpendicular distance between the center of the base and the center of the concavity.
The dome's convex region, which may be referred to here as "ceiling" (in an analogy with architecture) has a radius of curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
rc given by
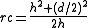
where d is the diameter and h is the height.
The kind of dome described so far is a spherical dome, though there are variants, such as the spheroidal dome, obtained by sectioning off a portion of a spheroid
Spheroid
A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters....
so that the resulting dome is symmetrical (having an axis of rotation), and likewise the ellipsoidal dome derived from the ellipsoid.
The surface area of a spherical dome's ceiling is
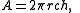
and the dome's volume is given by
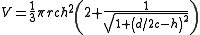
where r=d/2.