Double (manifold)
Encyclopedia
In the subject of manifold theory
in mathematics
, if
is a manifold with boundary, its double is obtained by gluing two copies of 
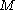together along their common boundary. Precisely, the double is 
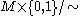where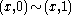 
for all 
.
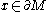Although the concept makes sense for any manifold, and even for some non-manifold sets such as the Alexander horned sphere
, the notion of double tends to be used primarily in the context that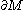
is non-empty and 
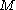is compact
.
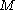, the double of 
is the boundary of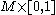 
. This gives doubles a special role in cobordism
.
is the double of the n-ball
. In this context, the two balls would be the upper and lower hemi-sphere respectively. More generally, if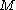
is closed, the double of 
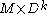is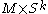 
. Even more generally, the double of a disc bundle over a manifold is a sphere bundle over the same manifold. More concretely, the double of the Möbius strip
is the Klein bottle
.
If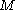
is a closed, oriented
manifold and if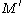
is obtained from 
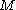by removing an open ball, then the connected sum
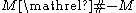is the double of 
.
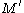The double of a Mazur manifold
is a homotopy 4-sphere
.
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, if
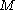is a manifold with boundary, its double is obtained by gluing two copies of together along their common boundary. Precisely, the double is 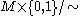where 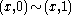for all 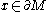.Although the concept makes sense for any manifold, and even for some non-manifold sets such as the Alexander horned sphere
Alexander horned sphere
The Alexander horned sphere is a wild embedding of a sphere into space, discovered by . It is the particular embedding of a sphere in 3-dimensional Euclidean space obtained by the following construction, starting with a standard torus:...
, the notion of double tends to be used primarily in the context that
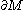is non-empty and 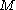is compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
.
Doubles bound
Given a manifold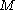, the double of is the boundary of 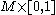. This gives doubles a special role in cobordismCobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
.
Examples
The n-sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
is the double of the n-ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
. In this context, the two balls would be the upper and lower hemi-sphere respectively. More generally, if
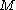is closed, the double of 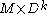is 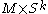. Even more generally, the double of a disc bundle over a manifold is a sphere bundle over the same manifold. More concretely, the double of the Möbius stripMöbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
is the Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
.
If
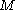is a closed, orientedOrientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
manifold and if
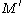is obtained from 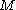by removing an open ball, then the connected sumConnected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
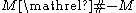is the double of 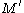.The double of a Mazur manifold
Mazur manifold
In differential topology, a branch of mathematics, a Mazur manifold is a contractible, compact, smooth 4-dimensional manifold which is not diffeomorphic to the standard 4-ball...
is a homotopy 4-sphere
Homotopy sphere
In algebraic topology, a branch of mathematics, a homotopy sphere is an n-manifold homotopy equivalent to the n-sphere. It thus has the same homotopy groups and the same homology groups, as the n-sphere...
.