Cobordism - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, cobordism is a fundamental equivalence relation

Equivalence relation

In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...

on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

. Two manifolds are cobordant if their disjoint union

Disjoint union

In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...

is the boundary of a manifold one dimension higher. The name comes from the French word for boundary. The boundary of an

-dimensional manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

is an

-dimensional manifold

that is closed, i.e., with empty boundary. In general, a
closed manifold need not be a boundary: cobordism theory is the study of the difference between all closed manifolds and those that are boundaries. The theory was originally developed for smooth (i.e., differentiable) manifolds, but there are now also versions for piecewise-linear and topological manifolds.

A cobordism is a manifold

with boundary whose boundary is partitioned in two,

.

Cobordisms are studied both for the equivalence relation that they generate, and as objects in their own right. Cobordism is a much coarser equivalence relation than diffeomorphism

Diffeomorphism

In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...

or homeomorphism

Homeomorphism

In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...

of manifolds, and is significantly easier to study and compute. It is not possible to classify manifolds up to diffeomorphism

Diffeomorphism

or homeomorphism

Homeomorphism

in dimensions

– because the word problem for groups

Word problem for groups

In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...

cannot be solved - but it is possible to classify manifolds up to cobordism. Cobordisms are central objects of study in geometric topology

Geometric topology

In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...

and algebraic topology

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

. In geometric topology, cobordisms are intimately connected with Morse theory

Morse theory

In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...

, and h-cobordisms

H-cobordism

A cobordism W between M and N is an h-cobordism if the inclusion mapsare homotopy equivalences...

are fundamental in the study of high dimensional manifolds, namely surgery theory

Surgery theory

In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...

. In algebraic topology, cobordism theories are fundamental extraordinary cohomology theories, and categories of cobordisms are the domains of topological quantum field theories

Topological quantum field theory

A topological quantum field theory is a quantum field theory which computes topological invariants....

Definition

More formally, an

-dimensional cobordism is a quintuple

consisting of an

-manifold with boundary

, closed

-manifolds

and embedding

Embedding

In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....

with disjoint images such that

The terminology is usually abbreviated to

.

Every closed manifold

is the boundary of the non-compact manifold

. So for the purposes of cobordism theory only compact manifolds are considered.

The above is the most basic (unoriented) form of the definition. In most practical situations, the manifolds in question are oriented, or carry some additional G-structure

G-structure

In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....

. One defines "oriented cobordism" and "cobordism with G-structure", but there are various technicalities. In each particular case, cobordism is an equivalence relation on manifolds. A basic question is to determine the equivalence classes for this relationship, called the cobordism classes of manifolds. Under favourable technical conditions these form a graded ring called the cobordism ring

, with grading by dimension, addition by disjoint union and multiplication by cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

. The cobordism groups

are the coefficient groups of a generalised homology theory.

Manifolds with boundary

An n+1-dimensional manifold with boundary is a topological space that is a union of the interior and the boundary: each point in the interior has a neighbourhood homeomorphic to the Euclidean n+1-dimensional space

and each point in the boundary has a neighbourhood homeomorphic to the Euclidean n+1-dimensional half-space

. In both cases, the point corresponds to the origin

Additional geometric structure

In most applications, the manifold

comes with additional geometric structure, such as a map to some reference space, or additional bundle data. One then wants the surgery process to endow

with the same kind of additional structure. For instance, a standard tool in surgery theory

Surgery theory

is surgery on normal maps

Normal invariants

In mathematics, a normal map is a concept in geometric topology due to William Browder which is of fundamental importance in surgery theory. Given a Poincaré complex X, a normal map on X endows the space, roughly speaking, with some of the homotopy-theoretic global structure of a closed manifold...

: such a process changes a normal map to another normal map within the same bordism class.

The surgery construction of cobordisms

Recall that in general, if

are manifolds with boundary, then the boundary of the product manifold is

.

Now, given a manifold

of dimension

and an embedding

Embedding

In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....

, define the

-manifold

obtained by surgery

Surgery theory

, via cutting out the interior of

and gluing in

along their boundary

. The trace of the surgery

defines an elementary cobordism

. Note that

is obtained from

by surgery on

. This is called reversing the surgery.

Every cobordism is a union of elementary cobordisms, by the work of Morse

Marston Morse

Harold Calvin Marston Morse was an American mathematician best known for his work on the calculus of variations in the large, a subject where he introduced the technique of differential topology now known as Morse theory...

, Thom

René Thom

René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...

and Milnor

John Milnor

John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...

Examples

1. The unit line

The unit line

is a 1-dimensional cobordism between the 0-dimensional manifolds

, and more generally for any closed manifold

there is defined a cobordism

from

.

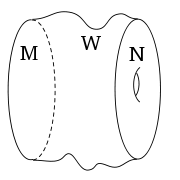
2. Pair of pants
If M consists of a circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

, and N of two circles, M and N together make up the boundary of a pair of pants

Pair of pants

In mathematics, a pair of pants is a simple two-dimensional surface resembling a pair of pants: topologically, it is a sphere with three holes in it...

W (see the figure at right).
Thus the pair of pants is a cobordism between M and N.

More generally, this picture shows that for any two

-dimensional manifolds

, the disjoint union

and connected sum

Connected sum

In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...

are cobordant, as the first corresponds to

and the latter to

The connected sum

is obtained from the disjoint union

by surgery
on an embedding

, and the cobordism is the trace
of the surgery.

3. Surgery on the Circle

As per the above definition, a surgery on the circle consists of cutting out a copy of

and glueing in

. The pictures in Fig. 1 show that the result of doing this is either (i)

again, or (ii) two copies of

4. Surgery on the 2-Sphere

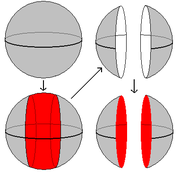
In this case there are more possibilities, since we can start by cutting out either

(a) : If we remove a cylinder from the 2-sphere, we are left with two disks. We have to glue back in - that is, two disks - and it's clear that the result of doing so is to give us two disjoint spheres. (Fig. 2a)

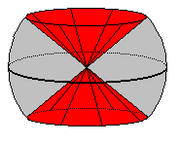
(b) : Having cut out two disks , we glue back in the cylinder . Interestingly, there are two possible outcomes, depending on whether our glueing maps have the same or opposite orientation on the two boundary circles. If the orientations are the same (Fig. 2b), the resulting manifold is the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

, but if they are different, we obtain the Klein Bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...

(Fig. 2c).

5. Morse functions

Suppose that

is a Morse function on an

-dimensional manifold, and suppose that

is a critical value with exactly one critical point in its preimage. If the index of this critical point is

, then the level-set

is obtained from

by a

-surgery. The inverse image

defines a cobordism

that can be identified with the trace of this surgery.

Manifolds that are not boundaries

The

-dimensional real projective space

Real projective space

In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...

RP²ⁿ is the simplest example of a (compact) closed manifold that is not the boundary of a manifold: the Euler characteristic

Euler characteristic

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

of a boundary must be even, but the Euler characteristic of RP²ⁿ is 1. More generally, any product of even-dimensional real projective spaces is not a boundary.

History

Cobordism had its roots in the (failed) attempt by Henri Poincaré

Henri Poincaré

Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...

in 1895 to define homology

Homology (mathematics)

In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...

purely in terms of manifolds . Poincaré
simultaneously defined both homology and cobordism, which are not the same, in general. See Cobordism as an extraordinary cohomology theory for the relationship between bordism and homology.

Bordism was explicitly introduced by Lev Pontryagin in geometric work on manifolds. It came to prominence when René Thom

René Thom

showed that cobordism groups could be computed by means of homotopy theory, via the Thom complex construction. Cobordism theory became part of the apparatus of extraordinary cohomology theory, alongside K-theory

K-theory

In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...

. It performed an important role, historically speaking, in developments in topology in the 1950s and early 1960s, in particular in the Hirzebruch-Riemann-Roch theorem

Hirzebruch-Riemann-Roch theorem

In mathematics, the Hirzebruch–Riemann–Roch theorem, named after Friedrich Hirzebruch, Bernhard Riemann, and Gustav Roch, is Hirzebruch's 1954 result contributing to the Riemann–Roch problem for complex algebraic varieties of all dimensions...

, and in the first proofs of the Atiyah-Singer index theorem.

In the 1980s the category with compact manifolds as objects and cobordisms between these as morphisms played a basic role in the Atiyah-Segal axioms for topological quantum field theory

Topological quantum field theory

A topological quantum field theory is a quantum field theory which computes topological invariants....

, which is an important part of quantum topology

Quantum topology

Quantum topology is a branch of mathematics that connects quantum mechanics with low-dimensional topology.Dirac notation provides a viewpoint of quantum mechanics which becomes amplified into a framework that can embrace the amplitudes associated with topological spaces and the related embedding of...

Context

Cobordisms are objects of study in their own right, apart from cobordism classes. Categorically

Category theory

Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...

, one can also think of a cobordism

as a map from M to N, and thus define categories of cobordisms. A cobordism is a kind of cospan: M → W ← N.

Terminology

An n-manifold M is called null-cobordant if there is a cobordism between M and the empty manifold; in other words, if M is the entire boundary of some (n+1)-manifold. Equivalently, its cobordism class is trivial.

For example:

The circle (and more generally, n-sphere) are null-cobordant since they bound an (n+1)-disk.
Every orientable surface is null-cobordant, because it is the boundary of a handlebody
Handlebody
In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...

.

Null-cobordisms with additional structure are called fillings
Symplectic filling
In mathematics, a filling of a manifold X is a cobordism W between X and the empty set. More to the point, the n-dimensional topological manifold X is the boundary of an n+1-dimensional manifold W...

.
"Bordism" and "cobordism" are sometimes used interchangeably; others distinguish them. When one wishes to distinguish the study of cobordism classes from the study of cobordisms as objects in their own right, one calls the equivalence question "bordism of manifolds", and the study of cobordisms as objects "cobordisms of manifolds".

The term "bordism" comes from French , meaning boundary. Hence bordism is the study of boundaries. "Cobordism" means "jointly bound", so M and N are cobordant if they jointly bound a manifold, i.e., if their disjoint union is a boundary. Further, cobordism groups form an extraordinary cohomology theory, hence the co-.

Geometry, and the connection with Morse theory and handlebodies

Given a cobordism

there exists a smooth function

such that

. By general position, one can assume

is Morse and such that all critical points occur in the interior of

. In this setting

is called a Morse function on a cobordism. The cobordism

is a union of the traces of a sequence of surgeries
on

, one for each critical point of

. The manifold

is obtained from

by attaching one handle for each critical point of

The Morse/Smale theorem states that for a Morse function on a cobordism, the flowlines of

give rise to a handle presentation of the triple

. Conversely, given a handle decomposition of a cobordism, it comes from a suitable Morse function. In a suitably normalized setting this process gives a correspondence between handle decompositions and Morse functions on a cobordism.

Development

This section covers cobordism of manifolds with different types of structures, and algebraic topological calculations concerned with these.

Cobordism classes

The general bordism problem is to calculate the cobordism classes of manifolds subject to various conditions.

-cobordism

When there is additional structure, the notion of cobordism must be formulated more precisely: a

-structure on

restricts to a

-structure on

and

. The basic examples are

for unoriented cobordism,

for oriented cobordism, and

for complex cobordism

Complex cobordism

In mathematics, complex cobordism is a generalized cohomology theory related to cobordism of manifolds. Its spectrum is denoted by MU. It is an exceptionally powerful cohomology theory, but can be quite hard to compute, so often instead of using it directly one uses some slightly weaker theories...

using stably complex manifold

Complex manifold

In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....

s. Many more are detailed by Stong.

Unoriented cobordism

The cobordism class

of a closed

-dimensional manifold

is determined by the Stiefel-Whitney characteristic numbers, which depend on the stable isomorphism class of the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

. Thus if

has a stably trivial tangent bundle then

. Every closed manifold

is such that

, so

for every

. In 1954 René Thom

René Thom

computed

with one generator

in each dimension

. For even

is possible to choose

, the cobordism class of the

-dimensional real projective space

Real projective space

.

The low-dimensional unoriented cobordism groups are

The mod2

Modular arithmetic

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....

Euler characteristic

of an unoriented

-dimensional manifold

is an unoriented cobordism invariant. For example, for any

The mod2 Euler characteristic map

is onto for all

, and an isomorphism for

Oriented cobordism

Assume all manifolds are oriented

Orientability

In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...

. Then an oriented cobordism is a manifold W whose boundary (with the induced orientations) is

, where

denotes

with the reversed orientation.

Why the reversed orientation? Firstly, because as oriented manifolds, the boundary of the cylinder

: both ends have opposite orientations (this is most familiar for the interval:

). It is also the correct definition in the sense of extraordinary cohomology theory.
For an oriented closed manifold

it is not in general the case that

is an oriented boundary, and the cobordism class

could
have infinite torsion, i.e., such that

for every
non-zero integer

The oriented cobordism groups are given modulo torsion by

,
the polynomial algebra generated by the oriented cobordism classes

of the complex projective space

Complex projective space

In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...

s (Thom, 1952)
The oriented cobordism group

is determined by the Stiefel-Whitney and Pontrjagin characteristic numbers (Wall, 1960). Two oriented manifolds are oriented cobordism if and only if
their Stiefel-Whitney and Pontrjagin numbers are the same.

The low-dimensional oriented cobordism groups are

The signature of an oriented

-dimensional manifold

is an oriented cobordism invariant, which is expressed in terms of the Pontrjagin numbers by
the Hirzebruch signature theorem.

For example, for any

The signature map

is onto for all

, and an isomorphism for

Cobordism as an extraordinary cohomology theory

Every vector bundle

Vector bundle

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...

theory (real, complex etc.) has a extraordinary cohomology theory called K-theory

K-theory

. Similarly, every cobordism theory

has an extraordinary cohomology theory, with homology ("bordism") groups

and cohomology ("cobordism") groups

for any space

. The generalized homology groups

are covariant in

, and the generalized cohomology groups

are contravariant in

. The cobordism groups defined above are, from this point of view, the homology groups of a point:

. Then

is the group of bordism classes of pairs

with

a closed

-dimensional manifold

(with G-structure) and

a map. Such pairs

are bordant if there exists a G-cobordism

with a map

, which restricts to

, and to

.

An

-dimensional manifold

has a fundamental homology class

Homology (mathematics)

In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...

(with coefficients in

in general, and in

in the oriented case), defining a natural transformation

which is far from being an isomorphism in general.

The bordism and cobordism theories of a space satisfy the Eilenberg-Steenrod axioms

Eilenberg-Steenrod axioms

In mathematics, specifically in algebraic topology, the Eilenberg–Steenrod axioms are properties that homology theories of topological spaces have in common...

apart from the dimension axiom. This does not mean that the groups

can be effectively computed once one knows the cobordism theory of a point and the homology of the space X, though the Atiyah-Hirzebruch spectral sequence

Atiyah-Hirzebruch spectral sequence

In mathematics, the Atiyah–Hirzebruch spectral sequence is a spectral sequence for calculating generalized cohomology, introduced by in the special case of K-theory. For a CW complex X, it relates the generalized cohomology groups...

gives a starting point for calculations. The computation is only easy if the particular cobordism theory reduces to a product of ordinary homology theories, in which case the bordism groups are the ordinary homology groups

.
This is true for unoriented cobordism. Other cobordism theories do not reduce to ordinary homology in this way, notably framed cobordism, oriented cobordism and complex cobordism

Complex cobordism

. The last-named theory in particular is much used by algebraic topologists as a computational tool (e.g., for the homotopy groups of spheres

Homotopy groups of spheres

In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting...

).
Cobordism theories are represented by Thom spectra

: given a group G, the Thom spectrum is composed from the Thom space

Thom space

In mathematics, the Thom space, Thom complex, or Pontryagin-Thom construction of algebraic topology and differential topology is a topological space associated to a vector bundle, over any paracompact space....

of the standard vector bundles

Tautological bundle

In mathematics, tautological bundle is a term for a particularly natural vector bundle occurring over a Grassmannian, and more specially over projective space...

over the classifying space

Classifying space

In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...

. Note that even for similar groups, Thom spectra can be very different:

and

are very different, reflecting the difference between oriented and unoriented cobordism.

From the point of view of spectra, unoriented cobordism is a product of Eilenberg-MacLane spectra –

– while oriented cobordism is a product of Eilenberg-MacLane spectra rationally, and at 2, but not at odd primes: the oriented cobordism spectrum

is rather more complicated than

Categories of cobordisms

Cobordisms form a category

Category theory

where the objects are closed manifolds and the morphisms are cobordisms. Composition is given by gluing together cobordisms end-to-end: the composition of

and

is defined by gluing the right end of the first to the left end of the second, yielding

.

A topological quantum field theory

Topological quantum field theory

A topological quantum field theory is a quantum field theory which computes topological invariants....

is a monoidal functor

Monoidal functor

In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a...

from a category of cobordisms to a category of vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

s. That is, it is a functor whose value on a disjoint union of manifolds is equivalent to the tensor product of its values on each of the constituent manifolds.

In low dimensions, the bordism question is trivial, but the category of cobordism is still interesting. For instance, the disk bounding the circle corresponds to a null-ary operation, while the cylinder corresponds to a 1-ary operation and the pair of pants to a binary operation.

Cobordism of piecewise linear and topological manifolds

Originally, cobordism was introduced for differentiable manifold

Differentiable manifold

A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...

s. The theory works also
for PL

Piecewise linear manifold

In mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...

and topological manifold

Topological manifold

In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...

s, with bordism groups

, which are generalized homology groups. The cobordism groups of PL and topological manifolds are harder to compute.

Definition

Manifolds with boundary

Additional geometric structure

The surgery construction of cobordisms

Examples

Manifolds that are not boundaries

History

Context

Terminology

Geometry, and the connection with Morse theory and handlebodies

Development

Cobordism classes

-cobordism

Unoriented cobordism

Oriented cobordism

Cobordism as an extraordinary cohomology theory

Categories of cobordisms

Cobordism of piecewise linear and topological manifolds

See also