Pair of pants
Encyclopedia
In mathematics
, a pair of pants is a simple two-dimensional surface
resembling a pair of pants
: topologically, it is a sphere with three holes in it. Pairs of pants admit hyperbolic metrics, and their isometry class is determined by the lengths of the boundary curves (the cuff lengths), or dually the distances between the boundaries (the seam lengths).
In hyperbolic geometry all three holes are considered equivalent – no distinction is made between "legs" and "waist". In cobordism
theory the holes are not equivalent – a pair of pants is a cobordism between one circle (the "waist") and two circles (the "legs").
, pairs of pants are sewn together, leg to leg, or leg to waist (there is no distinction between the legs and the waist), to create Riemann surface
s of arbitrary genus
; conversely, Riemann surfaces can be cut into pairs of pants by cutting along closed geodesics. Because the "legs" can be twisted before being sewn together, there is a large amount of freedom in how the pants can be assembled. This ambiguity gives the Fenchel–Nielsen coordinates
for the moduli space
of the Riemann surface, which has complex dimension 3(g − 1) = 3g − 3 for g > 1.
Formally, a pair of pants consists of two hexagonal fundamental polygon
s stitched together at every other side. Topologically, a pair of pants is the two-sphere S2 with three open disks removed, or equivalently the disk with two open disks removed. This is a deformation retract
of the thrice-punctured sphere (a sphere with three points removed), though these are not homeomorphic – the thrice-punctured spheres is not compact, and has no boundary components. Geometrically, a thrice-punctured sphere corresponds to pants where the cuff length is zero – where instead of a boundary circle, one has a cusp
– compare ideal triangle
.
A pair of pants, as a (subset of a) thrice-punctured sphere, admits a hyperbolic structure, unlike the unpunctured or once or twice punctured spheres (sphere, plane, annulus), which admit positive curvature, zero curvature, and zero curvature, respectively – compare Little Picard theorem.
It is homotopy
equivalent to the wedge sum
of two circles, and thus has fundamental group
isomorphic to the free group
on two generators (one generator for each circle).
A pair of pants is analogous to a fattened up hyperbolic triangle
, and is frequently so drawn schematically, with the seams as the sides and cuffs at vertices. Compare SSS and AAA congruence
of hyperbolic triangles to pairs of pants being determined by seam length or cuff lengths.
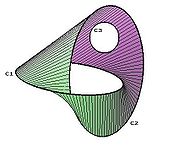In cobordism
theory, a pair of pants is a cobordism between a single circle and two circles (the waist and the legs), and, together with the fact that all compact connected 1-manifolds are circles, shows that the cobordism group of 1-manifolds is trivial. This also follows because a circle bounds a disk, and from this point of view a pair of pants is the connected sum
of a cylinder (identity cobordism of a circle) and a disk (null-cobordism of a circle).
(TQFT), a pair of pants corresponds to multiplication or comultiplication in a Frobenius algebra
, depending on which side is up, as follows.
An (n + 1)-dimensional TQFT, in Atiyah's axiomatization, is a symmetric monoidal functor from the category of (n + 1)-dimensional cobordism between n-dimensional manifolds to the category of vector spaces. In other words, it takes n-dimensional manifolds to vector spaces, disjoint unions of manifolds to tensor products of vector spaces, and cobordisms between manifolds to maps between vector spaces, satisfying suitable axioms. (1 + 1)-dimensional TQFTs correspond to Frobenius algebra
s, where the circle (the only connected closed 1-manifold) maps to the underlying vector space of the algebra, while the pair of pants gives a product or coproduct, depending on how the boundary components are grouped – which is commutative or cocommutative. Further, the map associated with a disk gives a counit (trace) or unit (scalars), depending on grouping of boundary, which completes the correspondence.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pair of pants is a simple two-dimensional surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
resembling a pair of pants
Trousers
Trousers are an item of clothing worn on the lower part of the body from the waist to the ankles, covering both legs separately...
: topologically, it is a sphere with three holes in it. Pairs of pants admit hyperbolic metrics, and their isometry class is determined by the lengths of the boundary curves (the cuff lengths), or dually the distances between the boundaries (the seam lengths).
In hyperbolic geometry all three holes are considered equivalent – no distinction is made between "legs" and "waist". In cobordism
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
theory the holes are not equivalent – a pair of pants is a cobordism between one circle (the "waist") and two circles (the "legs").
Hyperbolic geometry
In hyperbolic geometryHyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, pairs of pants are sewn together, leg to leg, or leg to waist (there is no distinction between the legs and the waist), to create Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s of arbitrary genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
; conversely, Riemann surfaces can be cut into pairs of pants by cutting along closed geodesics. Because the "legs" can be twisted before being sewn together, there is a large amount of freedom in how the pants can be assembled. This ambiguity gives the Fenchel–Nielsen coordinates
Fenchel–Nielsen coordinates
In mathematics, Fenchel–Nielsen coordinates are coordinates for Teichmüller space introduced by Werner Fenchel and Jakob Nielsen.-Definition:...
for the moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of the Riemann surface, which has complex dimension 3(g − 1) = 3g − 3 for g > 1.
Formally, a pair of pants consists of two hexagonal fundamental polygon
Fundamental polygon
In mathematics, each closed surface in the sense of geometric topology can be constructed from an even-sided oriented polygon, called a fundamental polygon, by pairwise identification of its edges....
s stitched together at every other side. Topologically, a pair of pants is the two-sphere S2 with three open disks removed, or equivalently the disk with two open disks removed. This is a deformation retract
Deformation retract
In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
of the thrice-punctured sphere (a sphere with three points removed), though these are not homeomorphic – the thrice-punctured spheres is not compact, and has no boundary components. Geometrically, a thrice-punctured sphere corresponds to pants where the cuff length is zero – where instead of a boundary circle, one has a cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
– compare ideal triangle
Ideal triangle
In hyperbolic geometry an ideal triangle is a hyperbolic triangle whose three vertices all lie on the circle at infinity. In the hyperbolic metric, any two ideal triangles are congruent...
.
A pair of pants, as a (subset of a) thrice-punctured sphere, admits a hyperbolic structure, unlike the unpunctured or once or twice punctured spheres (sphere, plane, annulus), which admit positive curvature, zero curvature, and zero curvature, respectively – compare Little Picard theorem.
It is homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
equivalent to the wedge sum
Wedge sum
In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
of two circles, and thus has fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
isomorphic to the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
on two generators (one generator for each circle).
A pair of pants is analogous to a fattened up hyperbolic triangle
Hyperbolic triangle
In mathematics, the term hyperbolic triangle has more than one meaning.-Hyperbolic geometry:In hyperbolic geometry, a hyperbolic triangle is a figure in the hyperbolic plane, analogous to a triangle in Euclidean geometry, consisting of three sides and three angles...
, and is frequently so drawn schematically, with the seams as the sides and cuffs at vertices. Compare SSS and AAA congruence
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
of hyperbolic triangles to pairs of pants being determined by seam length or cuff lengths.
Cobordism theory
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
theory, a pair of pants is a cobordism between a single circle and two circles (the waist and the legs), and, together with the fact that all compact connected 1-manifolds are circles, shows that the cobordism group of 1-manifolds is trivial. This also follows because a circle bounds a disk, and from this point of view a pair of pants is the connected sum
Connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
of a cylinder (identity cobordism of a circle) and a disk (null-cobordism of a circle).
Topological quantum field theory
In topological quantum field theoryTopological quantum field theory
A topological quantum field theory is a quantum field theory which computes topological invariants....
(TQFT), a pair of pants corresponds to multiplication or comultiplication in a Frobenius algebra
Frobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
, depending on which side is up, as follows.
An (n + 1)-dimensional TQFT, in Atiyah's axiomatization, is a symmetric monoidal functor from the category of (n + 1)-dimensional cobordism between n-dimensional manifolds to the category of vector spaces. In other words, it takes n-dimensional manifolds to vector spaces, disjoint unions of manifolds to tensor products of vector spaces, and cobordisms between manifolds to maps between vector spaces, satisfying suitable axioms. (1 + 1)-dimensional TQFTs correspond to Frobenius algebra
Frobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
s, where the circle (the only connected closed 1-manifold) maps to the underlying vector space of the algebra, while the pair of pants gives a product or coproduct, depending on how the boundary components are grouped – which is commutative or cocommutative. Further, the map associated with a disk gives a counit (trace) or unit (scalars), depending on grouping of boundary, which completes the correspondence.