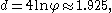In hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

 an ideal triangle is a hyperbolic triangle whose three vertices all lie on the circle at infinity. In the hyperbolic metric, any two ideal triangles are congruent

Congruence (geometry)

In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...

. Ideal triangles are also sometimes called triply asymptotic triangles or trebly asymptotic triangles.

Models

In the Poincaré disk model

Poincaré disk model

In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...

 of the hyperbolic plane, an ideal triangle is bounded by three circles which intersect the boundary circle at right angles. In the Poincaré half-plane model

Poincaré half-plane model

In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....

, an ideal triangle is modeled by an arbelos

Arbelos

In geometry, an arbelos is a plane region bounded by a semicircle of diameter 1, connected to semicircles of diameters r and , all oriented the same way and sharing a common baseline. Archimedes is believed to be the first mathematician to study its mathematical properties, as it appears in...

, the figure between three mutually tangent semicircle

Semicircle

In mathematics , a semicircle is a two-dimensional geometric shape that forms half of a circle. Being half of a circle's 360°, the arc of a semicircle always measures 180° or a half turn...

s. And in the Beltrami–Klein model of the hyperbolic plane, an ideal triangle is modeled by a Euclidean triangle that is circumscribed by the boundary circle. Note that in the Beltrami-Klein model, the angles at the vertices of an ideal triangle are not zero, because the Beltrami-Klein model, unlike the Poincaré disk and half-plane models, is not conformal

Conformal map

In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...

 i.e. it does not preserve angles.

Properties

In the standard hyperbolic plane (with Gaussian curvature

Gaussian curvature

In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...

 -1 at every point):

• The interior angles of an ideal triangle are all zero.
• Any ideal triangle has area π.
• Any ideal triangle has infinite perimeter.
• The inscribed circle to an ideal triangle meets the triangle in three points of tangency, forming an equilateral triangle with side length

where 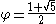is the golden ratio

Golden ratio

In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...

 http://www.cabri.net/abracadabri/GeoNonE/GeoHyper/KBModele/Biss3KB.html.

• The distance from any point in the triangle to the second-closest side of the triangle is less than or equal to d, with equality only for the three equilateral triangle vertices described above. The same inequality holds for hyperbolic triangles more generally; in a non-ideal triangle, the distance to the second-closest side is strictly less than d.

If the curvature is −K everywhere rather than −1, the areas above should be multiplied by 1/K and the lengths and distances should be multiplied by 1/√K.

Real ideal triangle group

The real ideal triangle group

Triangle group

In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...

 is the reflection group

Reflection group

In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...

generated by reflections of the hyperbolic plane through the sides of an ideal triangle. Algebraically, it is isomorphic to the free product of three order-two groups (Schwarz 2001).