In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, an arbelos is a plane region bounded by a semicircle

Semicircle

In mathematics , a semicircle is a two-dimensional geometric shape that forms half of a circle. Being half of a circle's 360°, the arc of a semicircle always measures 180° or a half turn...

 of diameter 1, connected to semicircles of diameters r and (1 − r), all oriented the same way and sharing a common baseline. Archimedes

Archimedes

Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...

 is believed to be the first mathematician to study its mathematical properties, as it appears in propositions four through eight of his Book of Lemmas

Book of Lemmas

The Book of Lemmas is a book attributed to Archimedes by Thābit ibn Qurra, though the authorship of the book is questionable. It consists of fifteen propositions on circles.-Translations:...

. Arbelos literally means "shoemaker's knife" in Greek; it resembles the blade of a knife used by ancient cobblers

Shoemaking

Shoemaking is the process of making footwear. Originally, shoes were made one at a time by hand. Traditional handicraft shoemaking has now been largely superseded in volume of shoes produced by industrial mass production of footwear, but not necessarily in quality, attention to detail, or...

.

Proof

If BC = 1 and BA = r, then

• In triangle BHA:
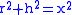
• In triangle CHA:
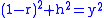
• In triangle BHC:

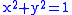
By substitution: 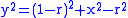. By expansion: 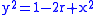. By substituting for y² into the equation for triangle BHC and solving for x: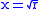
By substituting this, solve for y and h
The radius of the circle with center O is:
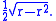
Therefore, the area is:
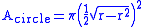
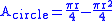
The area of the arbelos is the area of the large semicircle minus the area of the two smaller semicircles. Therefore the area of the arbelos is:
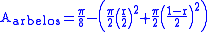
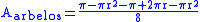
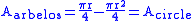
Q.E.D.

This property appears as Proposition 4 in Archimedes' Book of Lemmas:

If AB be the diameter of a semicircle and N any point on AB, and if semicircles be described within the first semicircle and having AN, BN as diameters respectively, the figure included between the circumferences of the three semicircles is [what Archimedes called "αρβελοσ"]; and its area is equal to the circle on PN as diameter, where PN is perpendicular to AB and meets the original semicircle in P.

Rectangle

The segment BH intersects the semicircle BA at D. The segment CH intersects the semicircle AC at E. Then DHEA is a rectangle

Rectangle

In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...

.

Proof: Angles BDA, BHC, and AEC are right angles because they are inscribed in semicircles (by Thales' theorem). The quadrilateral ADHE therefore has three right angles, so it is a rectangle. Q.E.D.

Tangents

The line DE is tangent to semicircle BA at D and semicircle AC at E.

Proof: Since angle BDA is a right angle, angle DBA equals π/2 minus angle DAB. However, angle DAH also equals π/2 minus angle DAB (since angle HAB is a right angle). Therefore triangles DBA and DAH are similar

Similarity (geometry)

Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...

. Therefore angle DIA equals angle DOH, where I is the midpoint of BA and O is the midpoint of AH. But AOH is a straight line, so angle DOH and DOA are supplementary angles

Supplementary angles

Supplementary angles are pairs of angles that add up to 180 degrees. Thus the supplement of an angle of x degrees is an angle of degrees....

. Therefore the sum of angles DIA and DOA is π. Angle IAO is a right angle. The sum of the angles in any quadrilateral is 2π, so in quadrilateral IDOA, angle IDO must be a right angle. But ADHE is a rectangle, so the midpoint O of AH (the rectangle's diagonal) is also the midpoint of DE (the rectangle's other diagonal). As I (defined as the midpoint of BA) is the center of semicircle BA, and angle IDE is a right angle, then DE is tangent to semicircle BA at D. By analogous reasoning DE is tangent to semicircle AC at E. Q.E.D.

See also

• Archimedes' circles
  Archimedes' circles
  In geometry, Archimedes' circles, first created by Archimedes, are two circles that can be created inside of an arbelos, both having the same area as each other.-Construction:...
  
  
• Archimedes' quadruplets
  Archimedes' quadruplets
  In geometry, Archimedes' quadruplets are four congruent circles associated with an arbelos. Introduced by Frank Power in the summer of 1998, each have the same area as Archimedes' twin circles, making them Archimedean circles.-Construction:...
  
  
• Bankoff circle
  Bankoff circle
  In geometry, the Bankoff circle or Bankoff triplet circle is a certain Archimedean circle that can be constructed from an arbelos; an Archimedean circle is any circle with area equal to each of Archimedes' twin circles. The Bankoff circle was first constructed by Leon Bankoff.-Construction:The...
  
  
• Ideal triangle
  Ideal triangle
  In hyperbolic geometry an ideal triangle is a hyperbolic triangle whose three vertices all lie on the circle at infinity. In the hyperbolic metric, any two ideal triangles are congruent...
  
  
• Schoch circles
  Schoch circles
  In geometry, the Schoch circles are twelve Archimedean circles constructed by Thomas Schoch.-History:In 1979, Thomas Schoch discovered a dozen new Archimedean circles; he sent his discoveries to Scientific American's "Mathematical Games" editor Martin Gardner. The manuscript was forwarded to Leon...
  
  
• Schoch line
  Schoch line
  In geometry, the Schoch line was created by Thomas Schoch. The line originated from Schoch's dozen circles.- Construction :With an arbelos two circular arcs K1 and K2 are created with the centers at point A and C, respectively. A circle, with the center A1, is then created tangent to the arcs...
  
  
• Woo circles
  Woo circles
  In geometry, the Woo circles, introduced by Peter Y. Woo, are a set of infinitely many Archimedean circles.-Construction:Form an arbelos with the two inner semicircles tangent at point C. Let m denote any nonnegative real number. Draw two circles, with radii m times the radius of the smaller two...
  
  
• Pappus chain
  Pappus chain
  In geometry, the Pappus chain was created by Pappus of Alexandria in the 3rd century AD.-Construction:The arbelos is defined by two circles, CU and CV, which are tangent at the point A and where CU is enclosed by CV...
  
  
• Salinon
  Salinon
  The salinon is a geometrical figure that consists of four semicircles. It was first introduced by Archimedes in his Book of Lemmas.-Construction:...
  
  

External links

• Arbelos – Amazing Properties (an interactive applet illustrating many Arbelos properties) at www.retas.de
• Arbelos at cut-the-knot
  Cut-the-knot
  Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...