In geometry

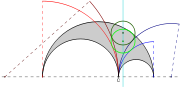
Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the Woo circles, introduced by Peter Y. Woo, are a set of infinitely many

Infinity

Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...

 Archimedean circles.

Construction

Form an arbelos

Arbelos

In geometry, an arbelos is a plane region bounded by a semicircle of diameter 1, connected to semicircles of diameters r and , all oriented the same way and sharing a common baseline. Archimedes is believed to be the first mathematician to study its mathematical properties, as it appears in...

 with the two inner semicircle

Semicircle

In mathematics , a semicircle is a two-dimensional geometric shape that forms half of a circle. Being half of a circle's 360°, the arc of a semicircle always measures 180° or a half turn...

s tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

 at point C. Let m denote any nonnegative real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

. Draw two circles, with radii m times the radius of the smaller two arbelos semicircles. centered on the arbelos ground line, also tangent to each other at point C and with radius m times the radius of the corresponding small arbelos arc. Any circle centered on the Schoch line

Schoch line

In geometry, the Schoch line was created by Thomas Schoch. The line originated from Schoch's dozen circles.- Construction :With an arbelos two circular arcs K1 and K2 are created with the centers at point A and C, respectively. A circle, with the center A1, is then created tangent to the arcs...

 and externally tangent to the circles

Tangent lines to circles

In Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...

is a Woo circle.