In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, an Archimedean circle is any circle constructed from an arbelos

Arbelos

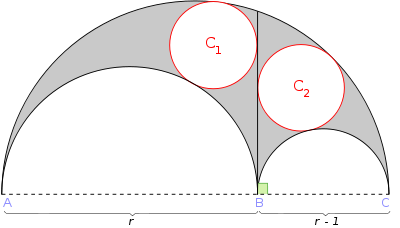
In geometry, an arbelos is a plane region bounded by a semicircle of diameter 1, connected to semicircles of diameters r and , all oriented the same way and sharing a common baseline. Archimedes is believed to be the first mathematician to study its mathematical properties, as it appears in...

 that has the same radius

Radius

In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

 as each of Archimedes' twin circles. The radius ρ of such a circle is given by
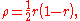
where r is the ratio AB/AC shown in the figure to the right. There are over fifty different known ways to construct Archimedean circles.

Origin

An Archimedean circle was first constructed by Archimedes

Archimedes

Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...

 in his Book of Lemmas

Book of Lemmas

The Book of Lemmas is a book attributed to Archimedes by Thābit ibn Qurra, though the authorship of the book is questionable. It consists of fifteen propositions on circles.-Translations:...

. In his book, he constructed what is now known as Archimedes' twin circles.

Leon Bankoff

Leon Bankoff

Leon Bankoff

Leon Bankoff , born in New York City, New York, was an American dentist and mathematician.- Life :...

 has constructed other Archimedean circles called Bankoff's triplet circle

Bankoff circle

In geometry, the Bankoff circle or Bankoff triplet circle is a certain Archimedean circle that can be constructed from an arbelos; an Archimedean circle is any circle with area equal to each of Archimedes' twin circles. The Bankoff circle was first constructed by Leon Bankoff.-Construction:The...

 and Bankoff's quadruplet circle.

Thomas Schoch

In 1978 Thomas Schoch found a dozen more Archimedean circles (the Schoch circles

Schoch circles

In geometry, the Schoch circles are twelve Archimedean circles constructed by Thomas Schoch.-History:In 1979, Thomas Schoch discovered a dozen new Archimedean circles; he sent his discoveries to Scientific American's "Mathematical Games" editor Martin Gardner. The manuscript was forwarded to Leon...

) that have been published in 1998. He also constructed what is known as the Schoch line

Schoch line

In geometry, the Schoch line was created by Thomas Schoch. The line originated from Schoch's dozen circles.- Construction :With an arbelos two circular arcs K1 and K2 are created with the centers at point A and C, respectively. A circle, with the center A1, is then created tangent to the arcs...

.

Peter Y. Woo

Peter Y. Woo considered the Schoch line, and with it, he was able to create a family of infinitely many Archimedean circles known as the Woo circles

Woo circles

In geometry, the Woo circles, introduced by Peter Y. Woo, are a set of infinitely many Archimedean circles.-Construction:Form an arbelos with the two inner semicircles tangent at point C. Let m denote any nonnegative real number. Draw two circles, with radii m times the radius of the smaller two...

.

Frank Power

In the summer of 1998, Frank Power introduced four more Archimedes circles known as Archimedes' quadruplets

Archimedes' quadruplets

In geometry, Archimedes' quadruplets are four congruent circles associated with an arbelos. Introduced by Frank Power in the summer of 1998, each have the same area as Archimedes' twin circles, making them Archimedean circles.-Construction:...

.