In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the Bankoff circle or Bankoff triplet circle is a certain Archimedean circle that can be constructed from an arbelos

Arbelos

In geometry, an arbelos is a plane region bounded by a semicircle of diameter 1, connected to semicircles of diameters r and , all oriented the same way and sharing a common baseline. Archimedes is believed to be the first mathematician to study its mathematical properties, as it appears in...

; an Archimedean circle is any circle with area equal to each of Archimedes' twin circles. The Bankoff circle was first constructed by Leon Bankoff

Leon Bankoff

Leon Bankoff , born in New York City, New York, was an American dentist and mathematician.- Life :...

.

Construction

The Bankoff circle is formed from three semicircle

Semicircle

In mathematics , a semicircle is a two-dimensional geometric shape that forms half of a circle. Being half of a circle's 360°, the arc of a semicircle always measures 180° or a half turn...

s that create an arbelos

Arbelos

In geometry, an arbelos is a plane region bounded by a semicircle of diameter 1, connected to semicircles of diameters r and , all oriented the same way and sharing a common baseline. Archimedes is believed to be the first mathematician to study its mathematical properties, as it appears in...

. A circle C₁ is then formed tangent to each of the three semicircles, as an instance of the problem of Apollonius

Problem of Apollonius

In Euclidean plane geometry, Apollonius' problem is to construct circles that are tangent to three given circles in a plane . Apollonius of Perga posed and solved this famous problem in his work ; this work has been lost, but a 4th-century report of his results by Pappus of Alexandria has survived...

. Another circle C₂ is then created, through three points: the two points of tangency of C₁ with the smaller two semicircles, and the point where the two smaller semicircles are tangent to each other. C₂ is the Bankoff circle.

Radius of the circle

If r = AB/AC, then the radius of the Bankoff circle is: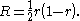

External links

• Bankoff Circle by Jay Warendorff, the Wolfram Demonstrations Project
  Wolfram Demonstrations Project
  The Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
  
  .
• Online catalogue of Archimedean circles, Floor van Lamoen.