The salinon is a geometrical figure that consists of four semicircle

Semicircle

In mathematics , a semicircle is a two-dimensional geometric shape that forms half of a circle. Being half of a circle's 360°, the arc of a semicircle always measures 180° or a half turn...

s. It was first introduced by Archimedes

Archimedes

Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...

 in his Book of Lemmas

Book of Lemmas

The Book of Lemmas is a book attributed to Archimedes by Thābit ibn Qurra, though the authorship of the book is questionable. It consists of fifteen propositions on circles.-Translations:...

.

Construction

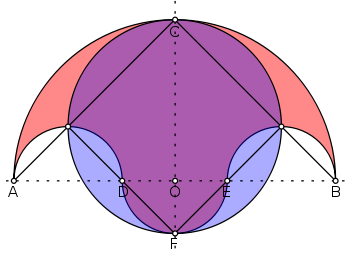
Let O be the origin on a Cartesian plane. Let A, D, E, and B be four points on a line, in that order, with O bisecting line AB. Let AD = EB. Semicircles are drawn above line AB with diameter

Diameter

In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...

s AB, AD, and EB, and another semicircle is drawn below with diameter DE. A salinon is the figure bounded by these four semicircles.

Area

Archimedes introduced the salinon in his Book of Lemmas by applying Book II, Proposition 10 of Euclid's Elements

Euclid's Elements

Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...

. Archimedes noted that "the area of the figure bounded by the circumferences of all the semicircles [is] equal to the area of the circle on CF as diameter."

Namely, the area of the salinon is:

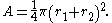
Proof

Let the radius of the midpoint

Midpoint

The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...

 of AD and EB be denoted as G and H, respectively. Therefore, AG = GD = EH = HB = r₁. Because DO, OF, and OE are all radii to the same semicircle, DO = OF = OE = r₂. By segment addition, AG + GD + DO = OE + EH + HB = 2r₁ + r₂. Since AB is the diameter of the salinon, CF is the line of symmetry. Because they all are radii of the same semicircle, AO = BO = CO = 2r₁ + r₂.

Let P be the center of the large circle. Because CO = 2r₁ + r₂ and OF = r₂, CF = 2r₁ + 2r₂. Therefore, the radius of the circle is r₁ + r₂. The area of the circle = π(r₁ + r₂)².

Let x = r₁ and y = r₂. The area of the semicircle with diameter AB is:
.

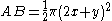The area of the semicircle with diameter DE is:


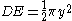
The area of each of the semicircles with diameters AD and EB is


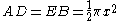
Therefore, the area of the salinon is:


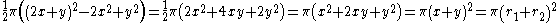
Q.E.D.

Arbelos

Should points D and E converge with O, it would form an arbelos

Arbelos

In geometry, an arbelos is a plane region bounded by a semicircle of diameter 1, connected to semicircles of diameters r and , all oriented the same way and sharing a common baseline. Archimedes is believed to be the first mathematician to study its mathematical properties, as it appears in...

, another one of Archimedes' creations, with symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

 among the y-axis.