
Link concordance
Encyclopedia
In mathematics
two links
 and
and  are concordant if there is an embedding
are concordant if there is an embedding
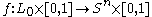 such that
such that 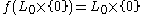 and
and 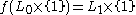 .
.
By its nature, link concordance is an equivalence relation
. It is weaker than isotopy, and stronger than homotopy
: isotopy implies concordance implies homotopy. A link is a slice link if it is concordant to the unlink
.
The linking number
of any two components of a link is one of the most elementary concordance invariants. The signature of a knot
is also a concordance invariant. A subtler concordance invariant are the Milnor invariants, and in fact all rational finite type
concordance invariants are Milnor invariants and their products, though non-finite type concordance invariants exist.
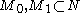 . In this case one considers two submanifolds concordant if there is a cobordism
. In this case one considers two submanifolds concordant if there is a cobordism
between them in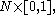 i.e., if there is a manifold with boundary
i.e., if there is a manifold with boundary 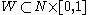 whose boundary consists of
whose boundary consists of 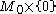 and
and 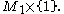
This higher dimensional concordance is a relative form of cobordism – it requires two submanifolds to be not just abstractly cobordant, but "cobordant in N".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
two links
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
 and
and  are concordant if there is an embedding
are concordant if there is an embeddingEmbedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
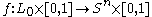 such that
such that 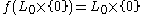 and
and 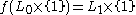 .
.By its nature, link concordance is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
. It is weaker than isotopy, and stronger than homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
: isotopy implies concordance implies homotopy. A link is a slice link if it is concordant to the unlink
Unlink
In the mathematical field of knot theory, the unlink is a link that is equivalent to finitely many disjoint circles in the plane.- Properties :...
.
Concordance invariants
A function of a link that is invariant under concordance is called a concordance invariants.The linking number
Linking number
In mathematics, the linking number is a numerical invariant that describes the linking of two closed curves in three-dimensional space. Intuitively, the linking number represents the number of times that each curve winds around the other...
of any two components of a link is one of the most elementary concordance invariants. The signature of a knot
Signature of a knot
The signature of a knot is a topological invariant in knot theory. It may be computed from the Seifert surface.Given a knot K in the 3-sphere, it has a Seifert surface S whose boundary is K...
is also a concordance invariant. A subtler concordance invariant are the Milnor invariants, and in fact all rational finite type
Finite type invariant
In the mathematical theory of knots, a finite type invariant is a knot invariant that can be extended to an invariant of certain singular knots that vanishes on singular knots with m + 1 singularities and does not vanish on some singular knot with 'm' singularities...
concordance invariants are Milnor invariants and their products, though non-finite type concordance invariants exist.
Higher dimensions
One can analogously define concordance for any two submanifolds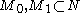 . In this case one considers two submanifolds concordant if there is a cobordism
. In this case one considers two submanifolds concordant if there is a cobordismCobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
between them in
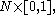 i.e., if there is a manifold with boundary
i.e., if there is a manifold with boundary 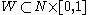 whose boundary consists of
whose boundary consists of 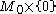 and
and 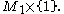
This higher dimensional concordance is a relative form of cobordism – it requires two submanifolds to be not just abstractly cobordant, but "cobordant in N".

