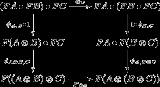
Monoidal functor
Encyclopedia
In category theory
, monoidal functors are functors between monoidal categories
which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors:
Although we distinguish between these different definitions here, authors may call any one of these simply monoidal functors.
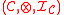and 
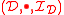be monoidal categories. A monoidal functor from 
to 
consists of a functor
together with a natural transformation
and a morphism
,
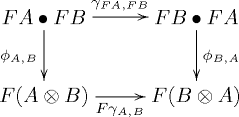
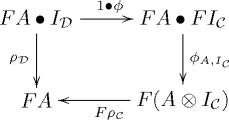
called the coherence maps or structure morphisms, which are such that for every three objects
, 
and 
of 
the diagrams
commute in the category
. Above, the various natural transformations denoted using 
are parts of the monoidal structure on 
and 
.
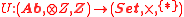from the category of abelian groups to the category of sets. In this case, the map 
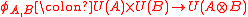is a surjection induced by the bilinearity relation, i.e. 
for 
; the map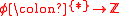 
sends * to 1.
is left adjoint to a monoidal 
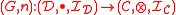. Then 
has a comonoidal structure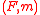 
induced by 
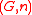, defined by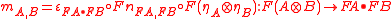
and
.
If the induced structure on
is strong, then the unit and counit of the adjunction are monoidal natural transformation
s, and the adjunction is said to be a monoidal adjunction
; conversely, the left adjoint of a monoidal adjunction is always a strong monoidal functor.
Similarly, a right adjoint to a comonoidal functor is monoidal, and the right adjoint of a comonoidal adjunction is a strong monoidal functor.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, monoidal functors are functors between monoidal categories
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors:
- The coherence maps of lax monoidal functors satisfy no additional properties; they are not necessarily invertible.
- The coherence maps of strong monoidal functors are invertible.
- The coherence maps of strict monoidal functors are identity maps.
Although we distinguish between these different definitions here, authors may call any one of these simply monoidal functors.
Definition
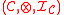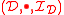Let and be monoidal categories. A monoidal functor from to consists of a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
together with a natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
and a morphism
,called the coherence maps or structure morphisms, which are such that for every three objects
, and of the diagrams
,
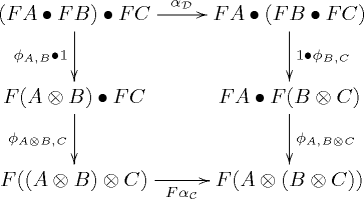and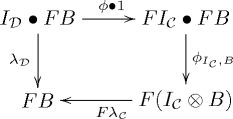 
commute in the category
. Above, the various natural transformations denoted using are parts of the monoidal structure on and .Variants
- The dual of a monoidal functor is a comonoidal functor; it is a monoidal functor whose coherence maps are reversed. Comonoidal functors may also be called opmonoidal, colax monoidal, or oplax monoidal functors.
- A strong monoidal functor is a monoidal functor whose coherence maps
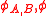are invertible. - A strict monoidal functor is a monoidal functor whose coherence maps are identities.
- A braided monoidal functor is a monoidal functor between braided monoidal categories such that the following diagram commutes for every pair of objects A, B in
:
- A symmetric monoidal functor is a braided monoidal functor whose domain and codomain are symmetric monoidal categories.
Example
The underlying functor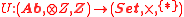 from the category of abelian groups to the category of sets. In this case, the map 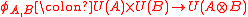is a surjection induced by the bilinearity relation, i.e. for ; the map 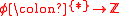sends * to 1.Monoidal functors and adjunctions
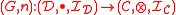Suppose that a functor is left adjoint to a monoidal . Then has a comonoidal structure 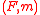induced by 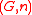, defined by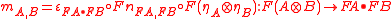and
.If the induced structure on
is strong, then the unit and counit of the adjunction are monoidal natural transformationMonoidal natural transformation
Suppose that and are two monoidal categories and:\to and :\toare two lax monoidal functors between those categories....
s, and the adjunction is said to be a monoidal adjunction
Monoidal adjunction
Suppose that and are two monoidal categories. A monoidal adjunction between two lax monoidal functors:\to and :\to...
; conversely, the left adjoint of a monoidal adjunction is always a strong monoidal functor.
Similarly, a right adjoint to a comonoidal functor is monoidal, and the right adjoint of a comonoidal adjunction is a strong monoidal functor.