
Monoidal adjunction
Encyclopedia
Suppose that 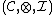 and
and  are two monoidal categories
are two monoidal categories
. A monoidal adjunction between two lax monoidal functors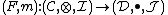 and
and 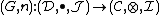
is an adjunction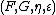 between the underlying functors, such that the natural transformation
between the underlying functors, such that the natural transformation
s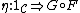 and
and 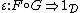
are monoidal natural transformation
s.
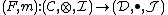
is a lax monoidal functor such that the underlying functor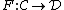 has a right adjoint
has a right adjoint 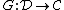 . This adjuction lifts to a monoidal adjuction
. This adjuction lifts to a monoidal adjuction  ⊣
⊣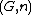 if and only if the lax monoidal functor
if and only if the lax monoidal functor 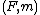 is strong.
is strong.
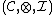 and
and  are two monoidal categories
are two monoidal categoriesMonoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
. A monoidal adjunction between two lax monoidal functors
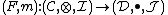 and
and 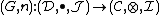
is an adjunction
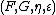 between the underlying functors, such that the natural transformation
between the underlying functors, such that the natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s
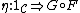 and
and 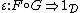
are monoidal natural transformation
Monoidal natural transformation
Suppose that and are two monoidal categories and:\to and :\toare two lax monoidal functors between those categories....
s.
Lifting adjunctions to monoidal adjunctions
Suppose that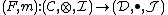
is a lax monoidal functor such that the underlying functor
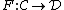 has a right adjoint
has a right adjoint 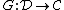 . This adjuction lifts to a monoidal adjuction
. This adjuction lifts to a monoidal adjuction  ⊣
⊣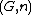 if and only if the lax monoidal functor
if and only if the lax monoidal functor 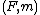 is strong.
is strong.See also
- Every monoidal adjunction
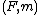 ⊣
⊣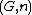 defines a monoidal monad
defines a monoidal monad 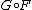 .
.

