Monoidal monad
Encyclopedia
In category theory
, a monoidal monad
is a monad
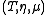on a monoidal category
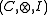such that the functor
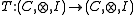
is a lax monoidal functor with
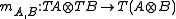
and
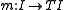
as coherence maps, and the natural transformations
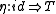
and
are monoidal natural transformation
s.
By monoidality of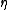
, the morphisms 
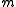and 
are necessarily equal.
This is equivalent to saying that a monoidal monad is a monad in the 2-category MonCat of monoidal categories, monoidal functors, and monoidal natural transformations.
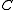and the Kleisli category is a monoidal adjunction
with respect to this monoidal structure.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a monoidal monad
is a monadMonad (category theory)
In category theory, a branch of mathematics, a monad, Kleisli triple, or triple is an functor, together with two natural transformations...
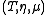on a monoidal categoryMonoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
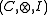such that the functor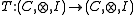is a lax monoidal functor with
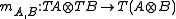
and
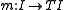
as coherence maps, and the natural transformations
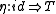
and
are monoidal natural transformation
Monoidal natural transformation
Suppose that and are two monoidal categories and:\to and :\toare two lax monoidal functors between those categories....
s.
By monoidality of
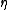, the morphisms 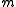and are necessarily equal.This is equivalent to saying that a monoidal monad is a monad in the 2-category MonCat of monoidal categories, monoidal functors, and monoidal natural transformations.
Properties
The Kleisli category of a monoidal monad has a canonical monoidal structure, induced by the monoidal structure of the monad. The canonical adjunction between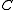 and the Kleisli category is a monoidal adjunctionMonoidal adjunction
Suppose that and are two monoidal categories. A monoidal adjunction between two lax monoidal functors:\to and :\to...
with respect to this monoidal structure.