
Hirzebruch-Riemann-Roch theorem
Encyclopedia
In mathematics
, the Hirzebruch–Riemann–Roch theorem, named after Friedrich Hirzebruch
, Bernhard Riemann
, and Gustav Roch
, is Hirzebruch's 1954 result contributing to the Riemann–Roch problem
for complex algebraic varieties of all dimensions. It was the first successful generalisation of the classical Riemann–Roch theorem
on Riemann surface
s to all higher dimensions, and paved the way to the Grothendieck–Hirzebruch–Riemann–Roch theorem
proved about three years later.
E on a compact
complex manifold
X, to calculate the holomorphic Euler characteristic of E in sheaf cohomology
, namely the alternating sum
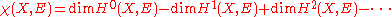
of the dimensions as complex vector spaces. (By basic results on coherent cohomology these dimensions are all finite, and are 0 except for the first 2n + 1 cases, where X has complex dimension
n, so the sum is finite.)
Hirzebruch's theorem states that χ(X, E) is computable in terms of the Chern class
es Cj(E) of E, and the Todd polynomials Tj in the Chern classes of the holomorphic tangent bundle
of X. These all lie in the cohomology ring
of X; by use of the fundamental class
(or, in other words, integration over X) we can obtain numbers from classes in H2n(X). The Hirzebruch formula asserts that

taken over all relevant j (so 0 ≤ j ≤ n), using the Chern character ch(E) in cohomology. In other words, the cross products are formed in cohomology ring of all the 'matching' degrees that add up to 2n, where to 'massage' the Cj(E) a formal manipulation is done, setting

and the total Chern class

Significant special cases are when E is a complex line bundle
, and when X is an algebraic surface
(Noether's formula). Weil's Riemann–Roch theorem for vector bundles on curves, and the Riemann–Roch theorem for algebraic surfaces (see below), are included in its scope. The formula also expresses in a precise way the vague notion that the Todd class
es are in some sense reciprocals of characteristic class
es.
. To see this,
recall that for each divisor
D on a curve there is an invertible sheaf
O(D) (which corresponds to a line bundle) such that
the linear system of D is more or less the space of sections of O(D).
For curves the Todd class is 1 + c1(T(X))/2, and the Chern character of a sheaf O(D) is just
1+c1(O(D)), so the Hirzebruch–Riemann–Roch theorem
states that
But h0(O(D)) is just l(D), the dimension of the linear system of D, and by Serre duality
h1(O(D)) = h0(O(K − D)) = l(K − D) where K is the canonical divisor. Moreover c1(O(D)) integrated over X is the degree of D, and c1(T(X)) integrated over X is the Euler class 2 − 2g
of the curve X, where g is the genus. So we get the classical Riemann Roch theorem
For vector bundles V, the Chern character is rank(V) + c1(V), so we get Weil's Riemann Roch theorem for vector bundles over curves:
combined with the Noether formula.
If we want, we can use Serre duality to express h2(O(D)) as h0(O(K − D)),
but unlike the case of curves there is in general no easy way to write the h1(O(D)) term in a form not involving sheaf cohomology (although in practice it often vanishes).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hirzebruch–Riemann–Roch theorem, named after Friedrich Hirzebruch
Friedrich Hirzebruch
Friedrich Ernst Peter Hirzebruch is a German mathematician, working in the fields of topology, complex manifolds and algebraic geometry, and a leading figure in his generation.-Life:He was born in Hamm, Westphalia...
, Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
, and Gustav Roch
Gustav Roch
Gustav Roch was a German mathematician who made significant contributions to the theory of Riemann surfaces in a career that was prematurely curtailed at the age of 26.-Biography:...
, is Hirzebruch's 1954 result contributing to the Riemann–Roch problem
Riemann–Roch theorem
The Riemann–Roch theorem is an important tool in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles...
for complex algebraic varieties of all dimensions. It was the first successful generalisation of the classical Riemann–Roch theorem
Riemann–Roch theorem
The Riemann–Roch theorem is an important tool in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles...
on Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s to all higher dimensions, and paved the way to the Grothendieck–Hirzebruch–Riemann–Roch theorem
Grothendieck–Hirzebruch–Riemann–Roch theorem
In mathematics, specifically in algebraic geometry, the Grothendieck–Riemann–Roch theorem is a far-reaching result on coherent cohomology. It is a generalisation of the Hirzebruch–Riemann–Roch theorem, about complex manifolds, which is itself a generalisation of the classical Riemann–Roch theorem...
proved about three years later.
Statement of Hirzebruch–Riemann–Roch theorem
The Hirzebruch–Riemann–Roch theorem applies to any holomorphic vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
E on a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
X, to calculate the holomorphic Euler characteristic of E in sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
, namely the alternating sum
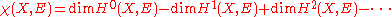
of the dimensions as complex vector spaces. (By basic results on coherent cohomology these dimensions are all finite, and are 0 except for the first 2n + 1 cases, where X has complex dimension
Complex dimension
In mathematics, complex dimension usually refers to the dimension of a complex manifold M, or complex algebraic variety V. If the complex dimension is d, the real dimension will be 2d...
n, so the sum is finite.)
Hirzebruch's theorem states that χ(X, E) is computable in terms of the Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
es Cj(E) of E, and the Todd polynomials Tj in the Chern classes of the holomorphic tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of X. These all lie in the cohomology ring
Cohomology ring
In mathematics, specifically algebraic topology, the cohomology ring of a topological space X is a ring formed from the cohomology groups of X together with the cup product serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is...
of X; by use of the fundamental class
Fundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
(or, in other words, integration over X) we can obtain numbers from classes in H2n(X). The Hirzebruch formula asserts that

taken over all relevant j (so 0 ≤ j ≤ n), using the Chern character ch(E) in cohomology. In other words, the cross products are formed in cohomology ring of all the 'matching' degrees that add up to 2n, where to 'massage' the Cj(E) a formal manipulation is done, setting

and the total Chern class

Significant special cases are when E is a complex line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
, and when X is an algebraic surface
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
(Noether's formula). Weil's Riemann–Roch theorem for vector bundles on curves, and the Riemann–Roch theorem for algebraic surfaces (see below), are included in its scope. The formula also expresses in a precise way the vague notion that the Todd class
Todd class
In mathematics, the Todd class is a certain construction now considered a part of the theory in algebraic topology of characteristic classes. The Todd class of a vector bundle can be defined by means of the theory of Chern classes, and is encountered where Chern classes exist — most notably...
es are in some sense reciprocals of characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es.
Riemann Roch theorem for curves
For curves, the Hirzebruch–Riemann–Roch theorem is essentially the classical Riemann–Roch theoremRiemann–Roch theorem
The Riemann–Roch theorem is an important tool in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles...
. To see this,
recall that for each divisor
Divisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
D on a curve there is an invertible sheaf
Invertible sheaf
In mathematics, an invertible sheaf is a coherent sheaf S on a ringed space X, for which there is an inverse T with respect to tensor product of OX-modules. It is the equivalent in algebraic geometry of the topological notion of a line bundle...
O(D) (which corresponds to a line bundle) such that
the linear system of D is more or less the space of sections of O(D).
For curves the Todd class is 1 + c1(T(X))/2, and the Chern character of a sheaf O(D) is just
1+c1(O(D)), so the Hirzebruch–Riemann–Roch theorem
states that
- h0(O(D)) − h1(O(D)) = c1(O(D)) +c1(T(X))/2 (integrated over X).
But h0(O(D)) is just l(D), the dimension of the linear system of D, and by Serre duality
Serre duality
In algebraic geometry, a branch of mathematics, Serre duality is a duality present on non-singular projective algebraic varieties V of dimension n . It shows that a cohomology group Hi is the dual space of another one, Hn−i...
h1(O(D)) = h0(O(K − D)) = l(K − D) where K is the canonical divisor. Moreover c1(O(D)) integrated over X is the degree of D, and c1(T(X)) integrated over X is the Euler class 2 − 2g
of the curve X, where g is the genus. So we get the classical Riemann Roch theorem
- l(D) − l(K − D) = deg(D) + 1 − g.
For vector bundles V, the Chern character is rank(V) + c1(V), so we get Weil's Riemann Roch theorem for vector bundles over curves:
- h0(V) − h1(V) = c1(V) + rank(V)(1 − g).
Riemann Roch theorem for surfaces
For surfaces, the Hirzebruch–Riemann–Roch theorem is essentially the Riemann–Roch theorem for surfacesRiemann–Roch theorem for surfaces
In mathematics, the Riemann–Roch theorem for surfaces describes the dimension of linear systems on an algebraic surface. The classical form of it was first given by , after preliminary versions of it were found by and...
- χ(D) = χ(O) + ((D.D) − (D.K))/2.
combined with the Noether formula.
If we want, we can use Serre duality to express h2(O(D)) as h0(O(K − D)),
but unlike the case of curves there is in general no easy way to write the h1(O(D)) term in a form not involving sheaf cohomology (although in practice it often vanishes).

