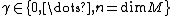Morse theory
Encyclopedia
In differential topology
, the techniques of Morse theory give a very direct way of analyzing the topology
of a manifold
by studying differentiable function
s on that manifold. According to the basic insights of Marston Morse
, a differentiable function on a manifold will, in a typical case, reflect the topology quite directly. Morse theory allows one to find CW structure
s and handle decompositions on manifolds and to obtain substantial information about their homology
.
Before Morse, Arthur Cayley
and James Clerk Maxwell
had developed some of the ideas of Morse theory in the context of topography
. Morse originally applied his theory to geodesic
s (critical point
s of the energy functional
on paths). These techniques were used in Raoul Bott
's proof of his celebrated periodicity theorem
.
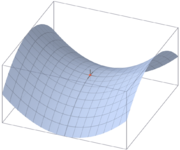Consider, for purposes of illustration, a mountainous landscape M. If f is the function
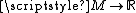sending each point
to its elevation, then the inverse image of a point in
(a level set
) is simply a contour line
. Each connected component of a contour line is either a point, a simple closed curve, or a closed curve with a double point
. Contour lines may also have points of higher order (triple points, etc.), but these are unstable and may be removed by a slight deformation of the landscape. Double points in contour lines occur at saddle points, or passes. Saddle points are points where the surrounding landscape curves up in one direction and down in the other.
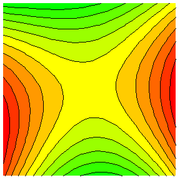Imagine flooding this landscape with water. Then, assuming the ground is porous, the region covered by water when the water reaches an elevation of a is f−1 (-∞, a] , or the points with elevation less than or equal to a. Consider how the topology of this region changes as the water rises. It appears, intuitively, that it does not change except when a passes the height of a critical point
; that is, a point where the gradient
of f is 0. In other words, it does not change except when the water either (1) starts filling a basin, (2) covers a saddle (a mountain pass
), or (3) submerges a peak.
To each of these three types of critical points - basins, passes, and peaks (also called minima, saddles, and maxima) - one associates a number called the index. Intuitively speaking, the index of a critical point b is the number of independent directions around b in which f decreases. Therefore, the indices of basins, passes, and peaks are 0, 1, and 2, respectively.
Define Ma as f−1(-∞, a] . Leaving the context of topography, one can make a similar analysis of how the topology of Ma changes as a increases when M is a torus
oriented as in the image and f is projection on a vertical axis, taking a point to its height above the plane.
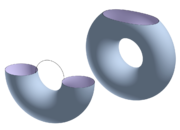Starting from the bottom of the torus, let p, q, r, and s be the four critical points of index 0, 1, 1, and 2, respectively. When a is less than 0, Ma is the empty set. After a passes the level of p, when 0<a<f(q), then Ma is a disk
, which is homotopy equivalent to a point (a 0-cell), which has been "attached" to the empty set. Next, when a exceeds the level of q, and f(q)<a<f(r), then Ma is a cylinder, and is homotopy equivalent to a disk with a 1-cell attached (image at left). Once a passes the level of r, and f(r)<a<f(s), then Ma is a torus with a disk removed, which is homotopy equivalent to a cylinder
with a 1-cell attached (image at right). Finally, when a is greater than the critical level of s, Ma is a torus. A torus, of course, is the same as a torus with a disk removed with a disk (a 2-cell) attached.
We therefore appear to have the following rule: the topology of Mα does not change except when α passes the height of a critical point, and when α passes the height of a critical point of index γ, a γ-cell is attached to Mα. This does not address the question of what happens when two critical points are at the same height. That situation can be resolved by a slight perturbation of f. In the case of a landscape (or a manifold embedded
in Euclidean space
), this perturbation might simply be tilting the landscape slightly, or rotating the coordinate system.
This rule, however, is false as stated. To see this, let M equal R and let f(x)=x3. Then 0 is a critical point of f, but the topology of Mα does not change when α passes 0. In fact, the concept of index does not make sense. The problem is that the second derivative is also 0 at 0. This kind of situation is called a degenerate critical point. Note that this situation is unstable: by rotating the coordinate system under the graph, the degenerate critical point either is removed or breaks up into two non-degenerate critical points.
f : M → R on a differentiable manifold
M, the points where the differential
of f vanishes are called critical point
s of f and their images under f are called critical value
s. If at a critical point b, the matrix of second partial derivatives (the Hessian matrix
) is non-singular, then b is called a non-degenerate critical point; if the Hessian is singular then b is a degenerate critical point.
For the functions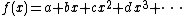
from R to R, f has a critical point at the origin if b=0, which is non-degenerate if c≠0 (i.e. f is of the form a+cx2+...) and degenerate if c=0 (i.e. f is of the form a+dx3+...).
A less trivial example of a degenerate critical point is the origin of the monkey saddle
.
The index
of a non-degenerate critical point b of f is the dimension of the largest subspace of the tangent space
to M at b on which the Hessian is negative definite. This corresponds to the intuitive notion that the index is the number of directions in which f decreases. The degeneracy and index of a critical point are independent of the choice the local coordinate system used, as shown by Sylvester's Law
.
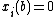for all 
and
throughout U. Here α is equal to the index of f at b. As a corollary of the Morse lemma we see that non-degenerate critical points are isolated
. (For a generalization, see Morse-Palais lemma
).
For functions from R2 to R with a critical point at the origin, the Morse lemma implies that after rotation of coordinates f will be of the form
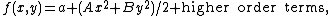
which will be degenerate if A = 0 or B = 0.
A smooth real-valued function on a manifold M is a Morse function if it has no degenerate critical points. A basic result of Morse theory says that almost all functions are Morse functions. Technically, the Morse functions form an open, dense subset of all smooth functions M → R in the C2 topology. This is sometimes expressed as "a typical function is Morse." or "a generic
function is Morse".
As indicated before, we are interested in the question of when the topology of Ma = f−1(-∞, a] changes as a varies. Half of the answer to this question is given by the following theorem.
It is also of interest to know how the topology of Ma changes when a passes a critical point. The following theorem answers that question.
These results generalize and formalize the 'rule' stated in the previous section. As was mentioned, the rule as stated is incorrect; these theorems correct it.
Using the two previous results and the fact that there exists a Morse function on any differentiable manifold, one can prove that any differentiable manifold is a CW complex with an n-cell for each critical point of index n. To do this, one needs the technical fact that one can arrange to have a single critical point on each critical level, which is usually proven by using gradient-like vector field
s to rearrange the critical points.
) it is clear that the Euler characteristic
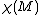is equal to the sum
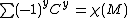
where Cγ is the number of critical points of index γ. Also by cellular homology, the rank of the nth homology group of a CW complex M is less than or equal to the number of n-cells in M. Therefore the rank of the γth homology group,i.e., the Betti number
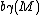, is less than or equal to the number of critical points of index γ of a Morse function on M. These facts can be strengthened to obtain the Morse inequalities:
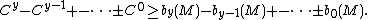
In particular, for any
we have
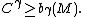
This gives a powerful tool to study manifold topology. Suppose on a closed manifold there exists a Morse function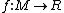
with precisely 
critical points. In what way does the existence of the function 
restricts 
? The case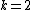 
was studied by Reeb in 1952; Reeb sphere theorem
states that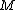
is homeomorphic to a sphere 
. The case 
is possible only in a small number of low dimensions, and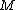 
is homeomorphic to an Eells–Kuiper manifold.
is a particularly easy way to understand approach to the homology
of smooth manifolds. It is defined using a generic choice of Morse function and Riemannian metric. The basic theorem is that the resulting homology is an invariant of the manifold (i.e. independent of the function and metric) and isomorphic to the singular homology of the manifold; this implies that the Morse and singular Betti number
s agree and gives an immediate proof of the Morse inequalities. An infinite dimensional analog of Morse homology is known as Floer homology
.
Ed Witten developed another related approach to Morse theory in 1982 using harmonic function
s.
(Equivalently, the kernel of the Hessian at a critical point equals the tangent space to the critical submanifold.)
A Morse function is the special case where the critical manifolds are zero-dimensional (so the Hessian at critical points is non-degenerate in every direction, i.e., has no kernel).
The index is most naturally thought of as a pair
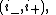
where i− is the dimension of the unstable manifold at a given point of the critical manifold, and i+ is i− plus the dimension of the critical manifold. If the Morse-Bott function is perturbed by a small function on the critical locus, the index of all critical points of the perturbed function on a critical manifold of the unperturbed function will lie between i− and i+).
Morse-Bott functions are useful because generic Morse functions are difficult to work with; the functions one can visualize, and with which one can easily calculate, typically have symmetries. They often lead to positive-dimensional critical manifolds. Raoul Bott
used Morse-Bott theory in his original proof of the Bott periodicity theorem
.
Round functions are examples of Morse-Bott functions, where the critical sets are
(disjoint unions of) circles.
Morse homology
can also be formulated for Morse-Bott functions; the differential in Morse-Bott homology is computed by a spectral sequence
. Frederic Bourgeois developed a neat approach in the course of his work on a Morse-Bott version of symplectic field theory.
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, the techniques of Morse theory give a very direct way of analyzing the topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
by studying differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s on that manifold. According to the basic insights of Marston Morse
Marston Morse
Harold Calvin Marston Morse was an American mathematician best known for his work on the calculus of variations in the large, a subject where he introduced the technique of differential topology now known as Morse theory...
, a differentiable function on a manifold will, in a typical case, reflect the topology quite directly. Morse theory allows one to find CW structure
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
s and handle decompositions on manifolds and to obtain substantial information about their homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
.
Before Morse, Arthur Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
and James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
had developed some of the ideas of Morse theory in the context of topography
Topography
Topography is the study of Earth's surface shape and features or those ofplanets, moons, and asteroids...
. Morse originally applied his theory to geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s (critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
s of the energy functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
on paths). These techniques were used in Raoul Bott
Raoul Bott
Raoul Bott, FRS was a Hungarian mathematician known for numerous basic contributions to geometry in its broad sense...
's proof of his celebrated periodicity theorem
Bott periodicity theorem
In mathematics, the Bott periodicity theorem describes a periodicity in the homotopy groups of classical groups, discovered by , which proved to be of foundational significance for much further research, in particular in K-theory of stable complex vector bundles, as well as the stable homotopy...
.
Basic concepts
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
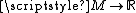sending each pointPoint (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
to its elevation, then the inverse image of a point in
(a level setLevel set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
) is simply a contour line
Contour line
A contour line of a function of two variables is a curve along which the function has a constant value. In cartography, a contour line joins points of equal elevation above a given level, such as mean sea level...
. Each connected component of a contour line is either a point, a simple closed curve, or a closed curve with a double point
Singular point of a curve
In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied.-Algebraic curves in the plane:...
. Contour lines may also have points of higher order (triple points, etc.), but these are unstable and may be removed by a slight deformation of the landscape. Double points in contour lines occur at saddle points, or passes. Saddle points are points where the surrounding landscape curves up in one direction and down in the other.
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
; that is, a point where the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of f is 0. In other words, it does not change except when the water either (1) starts filling a basin, (2) covers a saddle (a mountain pass
Mountain pass
A mountain pass is a route through a mountain range or over a ridge. If following the lowest possible route, a pass is locally the highest point on that route...
), or (3) submerges a peak.
Define Ma as f−1(-∞, a
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
oriented as in the image and f is projection on a vertical axis, taking a point to its height above the plane.
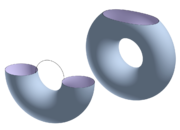
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
, which is homotopy equivalent to a point (a 0-cell), which has been "attached" to the empty set. Next, when a exceeds the level of q, and f(q)<a<f(r), then Ma is a cylinder, and is homotopy equivalent to a disk with a 1-cell attached (image at left). Once a passes the level of r, and f(r)<a<f(s), then Ma is a torus with a disk removed, which is homotopy equivalent to a cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
with a 1-cell attached (image at right). Finally, when a is greater than the critical level of s, Ma is a torus. A torus, of course, is the same as a torus with a disk removed with a disk (a 2-cell) attached.
We therefore appear to have the following rule: the topology of Mα does not change except when α passes the height of a critical point, and when α passes the height of a critical point of index γ, a γ-cell is attached to Mα. This does not address the question of what happens when two critical points are at the same height. That situation can be resolved by a slight perturbation of f. In the case of a landscape (or a manifold embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
), this perturbation might simply be tilting the landscape slightly, or rotating the coordinate system.
This rule, however, is false as stated. To see this, let M equal R and let f(x)=x3. Then 0 is a critical point of f, but the topology of Mα does not change when α passes 0. In fact, the concept of index does not make sense. The problem is that the second derivative is also 0 at 0. This kind of situation is called a degenerate critical point. Note that this situation is unstable: by rotating the coordinate system under the graph, the degenerate critical point either is removed or breaks up into two non-degenerate critical points.
Formal development
For a real-valued smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
f : M → R on a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
M, the points where the differential
Differential (calculus)
In calculus, a differential is traditionally an infinitesimally small change in a variable. For example, if x is a variable, then a change in the value of x is often denoted Δx . The differential dx represents such a change, but is infinitely small...
of f vanishes are called critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
s of f and their images under f are called critical value
Critical value
-Differential topology:In differential topology, a critical value of a differentiable function between differentiable manifolds is the image ƒ in N of a critical point x in M.The basic result on critical values is Sard's lemma...
s. If at a critical point b, the matrix of second partial derivatives (the Hessian matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
) is non-singular, then b is called a non-degenerate critical point; if the Hessian is singular then b is a degenerate critical point.
For the functions
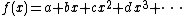
from R to R, f has a critical point at the origin if b=0, which is non-degenerate if c≠0 (i.e. f is of the form a+cx2+...) and degenerate if c=0 (i.e. f is of the form a+dx3+...).
A less trivial example of a degenerate critical point is the origin of the monkey saddle
Monkey saddle
In mathematics, the monkey saddle is the surface defined by the equation z = x^3 - 3xy^2. \, It belongs to the class of saddle surfaces and its name derives from the observation that a saddle for a monkey requires three depressions: two for the legs, and one for the tail...
.
The index
Index (mathematics)
The word index is used in variety of senses in mathematics.- General :* In perhaps the most frequent sense, an index is a number or other symbol that indicates the location of a variable in a list or array of numbers or other mathematical objects. This type of index is usually written as a...
of a non-degenerate critical point b of f is the dimension of the largest subspace of the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to M at b on which the Hessian is negative definite. This corresponds to the intuitive notion that the index is the number of directions in which f decreases. The degeneracy and index of a critical point are independent of the choice the local coordinate system used, as shown by Sylvester's Law
Sylvester's law of inertia
Sylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of coordinates...
.
The Morse lemma
Let b be a non-degenerate critical point of f : M → R. Then there exists a chart (x1, x2, ..., xn) in a neighborhood U of b such that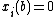 for all andthroughout U. Here α is equal to the index of f at b. As a corollary of the Morse lemma we see that non-degenerate critical points are isolated
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
. (For a generalization, see Morse-Palais lemma
Morse-Palais lemma
In mathematics, the Morse–Palais lemma is a result in the calculus of variations and theory of Hilbert spaces. Roughly speaking, it states that a smooth enough function near a critical point can be expressed as a quadratic form after a suitable change of coordinates.The Morse–Palais lemma was...
).
For functions from R2 to R with a critical point at the origin, the Morse lemma implies that after rotation of coordinates f will be of the form
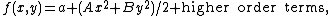
which will be degenerate if A = 0 or B = 0.
A smooth real-valued function on a manifold M is a Morse function if it has no degenerate critical points. A basic result of Morse theory says that almost all functions are Morse functions. Technically, the Morse functions form an open, dense subset of all smooth functions M → R in the C2 topology. This is sometimes expressed as "a typical function is Morse." or "a generic
Generic property
In mathematics, properties that hold for "typical" examples are called generic properties. For instance, a generic property of a class of functions is one that is true of "almost all" of those functions, as in the statements, "A generic polynomial does not have a root at zero," or "A generic...
function is Morse".
As indicated before, we are interested in the question of when the topology of Ma = f−1(-∞, a] changes as a varies. Half of the answer to this question is given by the following theorem.
- Theorem. Suppose f is a smooth real-valued function on M, a < b, f−1[a, b] is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, and there are no critical values between a and b. Then Ma is diffeomorphic to Mb, and Mb deformation retractDeformation retractIn topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
s onto Ma.
It is also of interest to know how the topology of Ma changes when a passes a critical point. The following theorem answers that question.
- Theorem. Suppose f is a smooth real-valued function on M and p is a non-degenerate critical point of f of index γ, and that f(p) = q. Suppose f−1[q − ε, q + ε] is compact and contains no critical points besides p. Then Mq + ε is homotopy equivalent to Mq − ε with a γ-cell attached.
These results generalize and formalize the 'rule' stated in the previous section. As was mentioned, the rule as stated is incorrect; these theorems correct it.
Using the two previous results and the fact that there exists a Morse function on any differentiable manifold, one can prove that any differentiable manifold is a CW complex with an n-cell for each critical point of index n. To do this, one needs the technical fact that one can arrange to have a single critical point on each critical level, which is usually proven by using gradient-like vector field
Gradient-like vector field
In differential topology, a mathematical discipline, and more specifically in Morse theory, a gradient-like vector field is a generalization of gradient vector field....
s to rearrange the critical points.
The Morse inequalities
Morse theory can be used to prove some strong results on the homology of manifolds. The number of critical points of index γ of f: M → R is equal to the number of γ cells in the CW structure on M obtained from "climbing" f. Using the fact that the alternating sum of the ranks of the homology groups of a topological space is equal to the alternating sum of the ranks of the chain groups from which the homology is computed, then by using the cellular chain groups (see cellular homologyCellular homology
In mathematics, cellular homology in algebraic topology is a homology theory for CW-complexes. It agrees with singular homology, and can provide an effective means of computing homology modules.- Definition :...
) it is clear that the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
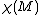is equal to the sum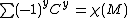where Cγ is the number of critical points of index γ. Also by cellular homology, the rank of the nth homology group of a CW complex M is less than or equal to the number of n-cells in M. Therefore the rank of the γth homology group,i.e., the Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
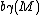, is less than or equal to the number of critical points of index γ of a Morse function on M. These facts can be strengthened to obtain the Morse inequalities: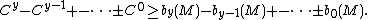In particular, for any
we have
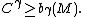
This gives a powerful tool to study manifold topology. Suppose on a closed manifold there exists a Morse function
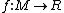with precisely critical points. In what way does the existence of the function restricts ? The case 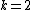was studied by Reeb in 1952; Reeb sphere theoremReeb sphere theorem
In mathematics, Reeb sphere theorem, named after Georges Reeb, states that-Morse foliation:A singularity of a foliation F is of Morse type if in its small neighborhood all leaves of the foliation are levels of a Morse function, being the singularity a critical point of the function...
states that
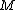is homeomorphic to a sphere . The case is possible only in a small number of low dimensions, and 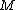is homeomorphic to an Eells–Kuiper manifold.Morse homology
Morse homologyMorse homology
In mathematics, specifically in the field of differential topology, Morse homology is a homology theory defined for any smooth manifold. It is constructed using the smooth structure and an auxiliary metric on the manifold, but turns out to be topologically invariant, and is in fact isomorphic to...
is a particularly easy way to understand approach to the homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of smooth manifolds. It is defined using a generic choice of Morse function and Riemannian metric. The basic theorem is that the resulting homology is an invariant of the manifold (i.e. independent of the function and metric) and isomorphic to the singular homology of the manifold; this implies that the Morse and singular Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s agree and gives an immediate proof of the Morse inequalities. An infinite dimensional analog of Morse homology is known as Floer homology
Floer homology
Floer homology is a mathematical tool used in the study of symplectic geometry and low-dimensional topology. First introduced by Andreas Floer in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory arising as an infinite dimensional analog of finite...
.
Ed Witten developed another related approach to Morse theory in 1982 using harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s.
Morse–Bott theory
The notion of a Morse function can be generalized to consider functions that have nondegenerate manifolds of critical points.Definition
A Morse–Bott function is a smooth function on a manifold whose critical set is a closed submanifold and whose Hessian is non-degenerate in the normal direction.(Equivalently, the kernel of the Hessian at a critical point equals the tangent space to the critical submanifold.)
A Morse function is the special case where the critical manifolds are zero-dimensional (so the Hessian at critical points is non-degenerate in every direction, i.e., has no kernel).
The index is most naturally thought of as a pair
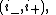
where i− is the dimension of the unstable manifold at a given point of the critical manifold, and i+ is i− plus the dimension of the critical manifold. If the Morse-Bott function is perturbed by a small function on the critical locus, the index of all critical points of the perturbed function on a critical manifold of the unperturbed function will lie between i− and i+).
Morse-Bott functions are useful because generic Morse functions are difficult to work with; the functions one can visualize, and with which one can easily calculate, typically have symmetries. They often lead to positive-dimensional critical manifolds. Raoul Bott
Raoul Bott
Raoul Bott, FRS was a Hungarian mathematician known for numerous basic contributions to geometry in its broad sense...
used Morse-Bott theory in his original proof of the Bott periodicity theorem
Bott periodicity theorem
In mathematics, the Bott periodicity theorem describes a periodicity in the homotopy groups of classical groups, discovered by , which proved to be of foundational significance for much further research, in particular in K-theory of stable complex vector bundles, as well as the stable homotopy...
.
Round functions are examples of Morse-Bott functions, where the critical sets are
(disjoint unions of) circles.
Morse homology
Morse homology
In mathematics, specifically in the field of differential topology, Morse homology is a homology theory defined for any smooth manifold. It is constructed using the smooth structure and an auxiliary metric on the manifold, but turns out to be topologically invariant, and is in fact isomorphic to...
can also be formulated for Morse-Bott functions; the differential in Morse-Bott homology is computed by a spectral sequence
Spectral sequence
In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
. Frederic Bourgeois developed a neat approach in the course of his work on a Morse-Bott version of symplectic field theory.
See also
- Discrete Morse theory
- Digital Morse theoryDigital Morse theoryIn mathematics, digital Morse theory is a digital adaptation of continuum Morse theory for scalar volume data.The main utility of a digital Morse theory is that it serves to provide a theoretical basis for isosurfaces, and perpendicular streamlines....
- Lusternik–Schnirelmann category
- Lagrangian GrassmannianLagrangian GrassmannianIn mathematics, the Lagrangian Grassmannian is the smooth manifold of Lagrangian subspaces of a real symplectic vector space V. Its dimension is n/2 . It may be identified with the homogeneous space...
- Morse–Smale systemMorse–Smale systemIn dynamical systems theory, an area of applied mathematics, a Morse–Smale system is a smooth dynamical system whose non-wandering set consists of finitely many hyperbolic equilibrium points and hyperbolic periodic orbits and satisfying a transversality condition on the stable and unstable manifolds...
- Sard's lemmaSard's lemmaSard's theorem, also known as Sard's lemma or the Morse–Sard theorem, is a result in mathematical analysis which asserts that the image of the set of critical points of a smooth function f from one Euclidean space or manifold to another has Lebesgue measure 0 – they form a null set...
- Stratified Morse theory