
Reeb sphere theorem
Encyclopedia
In mathematics
, Reeb sphere theorem, named after Georges Reeb
, states that
of a Morse function
, being the singularity a critical point
of the function. The singularity is a center if it is a local extremum
of the function; otherwise, the singularity is a saddle
.
The number of centers c and the number of saddles , specifically c − s, is tightly connected with the manifold topology.
, specifically c − s, is tightly connected with the manifold topology.
We denote ind p = min(k, n − k), the index of a singularity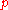 , where k is the index of the corresponding critical point of a Morse function. In particular, a center has index 0, index of a saddle is at least 1.
, where k is the index of the corresponding critical point of a Morse function. In particular, a center has index 0, index of a saddle is at least 1.
A Morse foliation F on a manifold M is a singular transversely oriented codimension one foliation of class C2 with isolated singularities such that:
Theorem: Let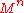 be a closed oriented connected manifold of dimension
be a closed oriented connected manifold of dimension  . Assume that
. Assume that  admits a
admits a 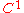 -transversely oriented codimension one foliation
-transversely oriented codimension one foliation  with a non empty set of singularities all of them centers. Then the singular set of
with a non empty set of singularities all of them centers. Then the singular set of  consists of two points and
consists of two points and 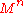 is homeomorphic to the sphere
is homeomorphic to the sphere 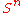 .
.
It is a consequence of the Reeb stability theorem
.

In 1978, E. Wagneur generalized the Reeb sphere theorem to Morse foliations with saddles. He showed that the number of centers cannot be too much as compared with the number of saddles, notably, . So there are exactly two cases when
. So there are exactly two cases when  :
:
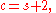

He obtained a description of the manifold admitting a foliation with singularities that satisfy (1).
Theorem: Let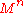 be a compact connected manifold admitting a Morse foliation
be a compact connected manifold admitting a Morse foliation  with
with  centers and
centers and  saddles. Then
saddles. Then  .
.
In case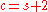 ,
,
Finally, in 2008, C. Camacho and B. Scardua considered the case (2),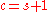 . Interestingly, this is possible in a small number of low dimensions.
. Interestingly, this is possible in a small number of low dimensions.
Theorem: Let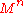 be a compact connected manifold and
be a compact connected manifold and  a Morse foliation on
a Morse foliation on  . If
. If 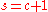 , then
, then
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Reeb sphere theorem, named after Georges Reeb
Georges Reeb
Georges Henri Reeb was a French mathematician. He worked in differential topology, differential geometry, differential equations, topological dynamical systems theory and non-standard analysis....
, states that
- A closed oriented connected manifold M n that admits a singular foliation having only centers is homeomorphicHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to the sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
Sn and the foliation has exactly two singularities.
Morse foliation
A singularity of a foliation F is of Morse type if in its small neighborhood all leaves of the foliation are levelsLevel set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
of a Morse function
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
, being the singularity a critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
of the function. The singularity is a center if it is a local extremum
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
of the function; otherwise, the singularity is a saddle
Saddle
A saddle is a supportive structure for a rider or other load, fastened to an animal's back by a girth. The most common type is the equestrian saddle designed for a horse, but specialized saddles have been created for camels and other creatures...
.
The number of centers c and the number of saddles
 , specifically c − s, is tightly connected with the manifold topology.
, specifically c − s, is tightly connected with the manifold topology.We denote ind p = min(k, n − k), the index of a singularity
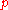 , where k is the index of the corresponding critical point of a Morse function. In particular, a center has index 0, index of a saddle is at least 1.
, where k is the index of the corresponding critical point of a Morse function. In particular, a center has index 0, index of a saddle is at least 1.A Morse foliation F on a manifold M is a singular transversely oriented codimension one foliation of class C2 with isolated singularities such that:
- each singularity of F is of Morse type,
- each singular leaf L contains a unique singularity p; in addition, if ind p = 1 then
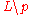 is not connected.
is not connected.
Reeb sphere theorem
This is the case c > s = 0, the case without saddles.Theorem: Let
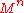 be a closed oriented connected manifold of dimension
be a closed oriented connected manifold of dimension  . Assume that
. Assume that  admits a
admits a 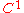 -transversely oriented codimension one foliation
-transversely oriented codimension one foliation  with a non empty set of singularities all of them centers. Then the singular set of
with a non empty set of singularities all of them centers. Then the singular set of  consists of two points and
consists of two points and 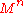 is homeomorphic to the sphere
is homeomorphic to the sphere 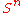 .
.It is a consequence of the Reeb stability theorem
Reeb stability theorem
In mathematics, Reeb stability theorem, named after Georges Reeb, asserts that if one leaf of a codimension-one foliation is closed and has finite fundamental group, then all the leaves are closed and have finite fundamental group....
.
Generalization
More general case is
In 1978, E. Wagneur generalized the Reeb sphere theorem to Morse foliations with saddles. He showed that the number of centers cannot be too much as compared with the number of saddles, notably,
 . So there are exactly two cases when
. So there are exactly two cases when  :
: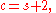

He obtained a description of the manifold admitting a foliation with singularities that satisfy (1).
Theorem: Let
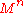 be a compact connected manifold admitting a Morse foliation
be a compact connected manifold admitting a Morse foliation  with
with  centers and
centers and  saddles. Then
saddles. Then  .
.In case
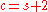 ,
,-
 is homeomorphic to
is homeomorphic to 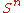 ,
,
- all saddles have index 1,
- each regular leaf is diffeomorphic to
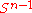 .
.
Finally, in 2008, C. Camacho and B. Scardua considered the case (2),
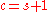 . Interestingly, this is possible in a small number of low dimensions.
. Interestingly, this is possible in a small number of low dimensions.Theorem: Let
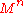 be a compact connected manifold and
be a compact connected manifold and  a Morse foliation on
a Morse foliation on  . If
. If 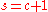 , then
, then-
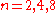 or
or 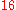 ,
,
-
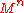 is an Eells–Kuiper manifold.
is an Eells–Kuiper manifold.

